Abstract
Background and Methodology:
The current Ebola virus epidemic in West Africa has been spreading at least since December 2013. The first confirmed case of Ebola virus in Sierra Leone was identified on May 25. Based on viral genetic sequencing data from 72 individuals in Sierra Leone collected between the end of May and mid June, we utilize a range of phylodynamic methods to estimate the basic reproductive number (R0). We additionally estimate the expected lengths of the incubation and infectious periods of the virus. Finally, we use phylogenetic trees to examine the role played by population structure in the epidemic.
Results:
The median estimates of R0 based on sequencing data alone range between 1.65-2.18, with the most plausible model yielding a median R0 of 2.18 (95% HPD 1.24-3.55). Importantly, our results indicate that, at least until mid June, relief efforts in Sierra Leone were ineffective at lowering the effective reproductive number of the virus. We estimate the expected length of the infectious period to be 2.58 days (median; 95% HPD 1.24-6.98). The dataset appears to be too small in order to estimate the incubation period with high certainty (median expected incubation period 4.92 days; 95% HPD 2.11-23.20). While our estimates of the duration of infection tend to be smaller than previously reported, phylodynamic analyses support a previous estimate that 70% of cases were observed and included in the present dataset. The dataset is too small to show a particular population structure with high significance, however our preliminary analyses suggest that half the population is spreading the virus with an R0 well above 2, while the other half of the population is spreading with an R0 below 1.
Conclusions:
Overall we show that sequencing data can robustly infer key epidemiological parameters. Such estimates inform public health officials and help to coordinate effective public health efforts. Thus having more sequencing data available for the ongoing Ebola virus epidemic and at the start of new outbreaks will foster a quick understanding of the dynamics of the pathogen.
Funding Statement
T.S. is supported in part by the European Research Council under the 7th Framework Programme of the European Commission (PhyPD: Grant Agreement Number 335529) and by the Swiss National Science foundation (PZ00P3_136820). D.K. is supported by an ETHZ Postdoctoral Fellowship. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.Introduction
The 2014 West African Ebola virus (EBOV) epidemic is the largest Ebola virus outbreak to date with 7492 cases (4108 confirmed) and 3439 deaths (2078 confirmed) as of 3 October 20141. While previous EBOV outbreaks remained localized, the current epidemic has spread across Guinea, Sierra Leone and Liberia with a localized outbreak in Nigeria. (Both Senegal and the USA have reported one imported case with no local transmission, as of 3 October 2014). Relief efforts have so far been ineffective at containing the disease, due largely to porous borders, a lack of education about the disease and degraded public health infrastructure2,3,4. Moreover, the epidemic has spread to major urban areas, further facilitating its continued spread and complicating containment efforts.
Patients exposed to EBOV first undergo an incubation period of 2-21 days before becoming infectious3,5,6,7. Once infectious, patients either die between days 6 and 16 or may begin to recover between days 6 and 113,8,9. Although patients who recover are generally noninfectious after convalescence, EBOV has been isolated 33 days after the onset of symptoms from mucosal membranes and 61 days after the onset of symptoms from semen10,11. There is currently no known effective treatment or vaccine for Ebola virus disease and relief efforts focus on bringing down the case fatality rate through supportive care and disease containment3.
In Gire et al. (2014)12, 99 Ebola genomes from 78 patients from the Sierra Leone outbreak are provided. This represents about 70% of confirmed cases during late May to mid June. Based on the phylogenies in Gire et al. (2014)12, it is likely that the Sierra Leone outbreak was started by the simultaneous introduction of two genetically distinct viruses. The initial 14 confirmed cases in Sierra Leone have all been epidemiologically linked to the funeral of a traditional healer in Guinea, supporting a single introduction event. The first split of the Sierra Leone sequences, separating the two introductions, is supported in all posterior trees presented in Gire et al. (2014)12 as well as in our preliminary analyses. We focused on the introduction causing the larger outbreak (72 sampled patients) and ignored the smaller outbreak (6 sampled patients).
We use these genomic data to estimate epidemiological parameters. We employed the Bayesian MCMC framework BEAST213 , applying a range of epidemiological tree priors to the sequencing data. The tree priors are based both on birth-death14 and coalescent15 models. Furthermore, we estimated epidemiological parameters based on the trees from Gire et al. (2014)12 using a maximum likelihood framework implemented in R16 .
Methods for epidemiological parameter inference
The boxes S, E, I and R refer to the host compartments for susceptible, exposed, infected and recovered/removed individuals, respectively. Rates with subscript k can change over time in a piecewise constant fashion.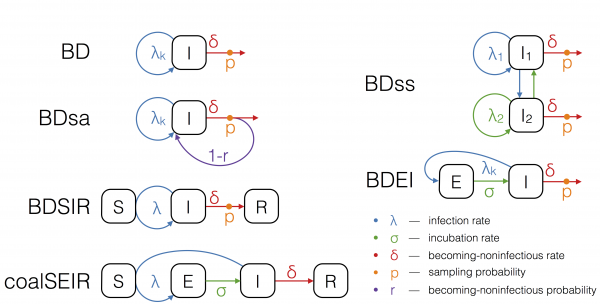
Fig. 1: The epidemiological models used for phylodynamic inference.
The larger outbreak, consisting of 72 Ebola sequences, is analysed in BEAST213 to estimate the epidemiological parameters relevant to the epidemic. We employ birth-death and coalescent approaches as models for epidemic spread.
Birth-death models assume a transmission rate with which infected individuals transmit, a becoming-noninfectious rate with which infected individuals recover or die, and a sampling probability, which is the probability at which an infectious person is sampled and sequenced. Such a model naturally accounts for incomplete sampling and, since the sampling probability is a parameter in our model, this quantity may also be estimated. In particular, we run birth-death analyses using the models depicted in Figure 1. We explain the assumptions of these models in the following.
The birth-death (BD) model17 allows the three parameters, transmission rate, becoming-noninfectious rate, and sampling probability to change in a piecewise constant fashion.
To model the spread of EBOV more realistically, we further extend the birth-death model to allow for an exposed class of infected people. The exposed class is entered upon infection, and an exposed individual moves from the exposed to the infectious class with a constant incubation rate. This model is referred to as the birth-death exposed-infected (BDEI) model18,19. In the BDEI model we assume that only infectious people are sampled, since exposed patients are asymptomatic.
BD and BDEI assume that individuals become noninfectious upon sampling. As Ebola may be transmitted also after sampling (transmission at funerals constitutes a major source of infection2,3,20) we further run the birth-death sampled-ancestors (BDsa) model21, which extends BD by assuming that sampled individuals become noninfectious upon sampling with probability r and remain infectious with probability 1-r. When r<1 the phylogeny may contain sampled ancestors, meaning samples do not have to coincide with tips in the tree, but a sample in the tree may have sampled descendants.
The BDSIR model22 is a variant of the BD model in which we explicitly account for susceptible hosts, meaning the epidemic slows down once the number of susceptible hosts declines. This model includes an explicit susceptible class and the number of initial susceptible hosts as a parameter, which was estimated using a LogNormal(8,4) prior distribution.
We also fit a deterministic coalescent model to the EBOV sequence data. We use the structured coalescent framework of Volz (2012)15, assuming an exposed and infectious class (as in the BDEI model), to probabilistically take into account whether lineages reside in exposed or infectious individuals. This coalescent SEIR model (coalSEIR) was implemented in BEAST2 and epidemiological parameters were estimated along with the genealogy from the sequence data, with the initial number of susceptible hosts set to 1 million, following Althaus (2014)23.
In all analyses we first assumed a constant basic reproductive number R0, which is the ratio of the transmission rate over the becoming-noninfectious rate. Second we allowed the reproductive number to change twice: at the time of the oldest sample (May 26) and midway between the oldest and youngest samples (June 6). The becoming-noninfectious rate and the sampling probability were assumed to remain constant throughout the epidemic outbreak.
We assumed the following Bayesian prior distributions for our analyses. The prior for R0 is LogNormal(0,1.25). The time of origin, i.e. the time of infection of the first person in the Sierra Leone outbreak, was assumed to be uniform during the 6 (and for computational reasons in some analyses, 3) months prior to the most recent sample at time 18 June 2014, thus any start time of the Sierra Leone outbreak from 18 December 2014 (or 18 March 2014) was equally likely. For the incubation rate and the becoming-noninfectious rate we assumed a Gamma prior with shape 0.5 and scale 1/6 days-1, truncated, such that the periods of being exposed and infectious lie between 1 and 26 days, and such that all times in this interval have considerable support. The median of these priors is 0.11 days-1, meaning that the expected time of being exposed and infectious is 9 days each. As no sequencing effort has been performed prior to the oldest sample, collected on 25 May 2014, we assume that the sampling probability is 0 prior to that date and constant afterwards. After that date, we assume a uniform prior on [0,1] for the sampling probability in the analyses without exposed class. To improve computational performance in the more complex BDEI model, we assume a Beta(70,30) prior distribution, supporting a sampling proportion around 70%, based on our own results as well as Gire et al. (2014)12 , and also fix the mean clock rate to 1.984e-3/site/year12 . The priors on all epidemiological parameters as well as the mean clock rate were identical between the coalSEIR and BDEI models.
Instead of reporting the becoming-noninfectious rate and the incubation rate, we report their inverse values, which are the expected times of being exposed (incubation time) and being infectious. We report the median posterior value for each parameter together with the shortest interval containing 95% of the posterior samples.
Maximum likelihood analysis using birth-death models
As a comparison, we performed maximum likelihood (ML) parameter estimation using the posterior trees from Gire et al. (2014)12. Again, we first eliminated the Guinea samples and the 6 samples from the second Sierra Leone outbreak. Thus all trees analyzed consist of 72 tips. From the 10001 posterior trees provided by the authors of Gire et al. (2014)12 , we eliminated the first 1001 trees as burn-in, and then chose every 100th tree from the remaining 9000 trees, yielding a set of 90 trees. For these 90 trees, we performed an analysis under the BD model with constant and time-varying reproductive number and BDEI with constant R0 using the R package TreePar v3.116. Additionally, we applied a birth-death model to the trees quantifying the amount of superspreading in the population, BDss18. This model extends the constant-rate BD model, assuming that individuals belong to either one of two classes with a unique R0. Individuals transmit to both classes. We report the median maximum likelihood value together with the shortest interval containing 95% of the ML estimates from all 90 trees.
Epidemiological parameter estimates
(A) R0, (B) incubation period and (C) infectious period. The estimates from methods allowing the reproductive number to change over time are omitted. We also omit estimates from models where we fixed any of the other model parameters (except for the maximum-likelihood estimates, where the sampling probability is always fixed).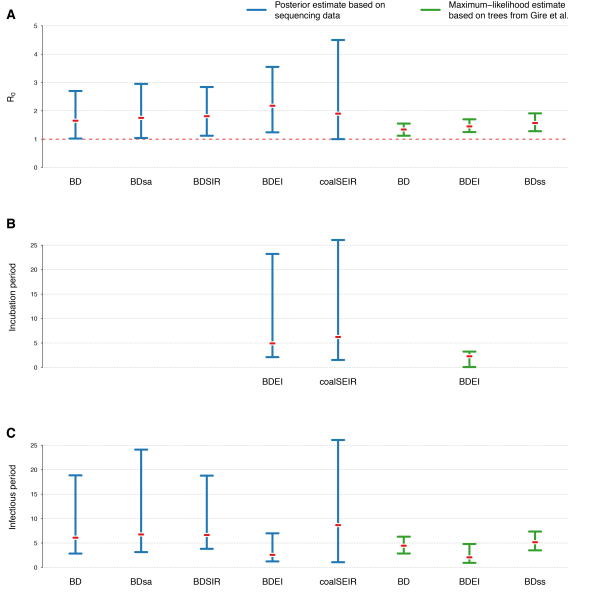
Fig. 2: 95% HPD intervals of estimated parameters for different phylodynamic methods
Figure 2 displays the estimated R0 values for the different phylodynamic methods. Overall the different Bayesian methods simultaneously inferring trees and parameters yield median estimates between 1.65-2.18. The maximum likelihood methods inferring parameters based on fixed trees obtain lower estimates. In the following we discuss the results in detail.
Bayesian birth-death analysis
Models followed by 1 estimate only a constant R0, while models followed by 3 allow the reproductive number to change 3 times over the course of the epidemic.
*Sampling probability prior: Beta(70,30), mean clock rate fixed to 1.984e-3 [Gire 2014], origin prior: Unif(0,3months)
R0/Re initial
Re
middle
Re
recent
Incubation
time (days)Infectious
time (days)Sampling
probabilityEpidemic
originTree
MRCA
BD 1
1.65
(1.02-2.70)
–
–
–
6.09
(2.84-18.84)
0.65
(0.20-1.00)
May 7
(7/4-22/5)
May 15
(3/5-22/5)
BD 3
0.95
(0.22-2.56)
1.57
(0.73-2.91)
1.81
(1.07-3.03)
–
6.15
(3.22-17.94)
0.70
(0.27-1.00)
April 8
(30/12-21/5)
May 12
(24/4-23/5)
BDsa 1
1.75
(1.04-2.95)
–
–
–
6.75
(3.14-24.10)
0.60
(0.17-1.00)
May 8
(10/4-22/5)
May 15
(3/5-23/5)
BDsa 3
0.96
(0.20-2.65)
1.61
(0.74-3.00)
1.88
(1.09-3.23)
–
6.54
(3.24-22.10)
0.65
(0.19-1.00)
April 9
(31/12-20/5)
May 12
(24/4-23/5)
BDSIR
1.81
(1.12-2.84)
–
–
–
6.64
(3.61-18.78)
0.70
(0.24-1.00)
May 4
(11/4-19/5)
May 15
(3/5-22/5)
BDEI 1*
2.18
(1.46-3.22)
–
–
5.6
(fixed)
2.29
(1.23-5.62)
0.72
(0.63-0.80)
May 10
(13/4-23/5)
May 14
(3/5-22/5)
BDEI 3*
1.77
(0.59-4.35)
1.92
(0.80-3.64)
2.86
(1.58-4.78)
5.6
(fixed)
2.75
(1.41-7.07)
0.71
(0.62-0.79)
May 8
(14/3-22/5)
May 13
(28/4-22/5)
BDEI 1*
1.85
(1.17-2.76)
–
–
2.3
(fixed)
3.92
(2.15-9.47)
0.71
(0.62-0.79)
May 9
(15/4-21/5)
May 14
(4/5-22/5)
BDEI 3*
1.63
(0.54-4.09)
1.66
(0.71-3.13)
2.45
(1.28-4.17)
2.3
(fixed)
4.72
(2.46-10.74)
0.71
(0.62-0.79)
May 5
(12/3-23/5)
May 13
(29/4-22/5)
BDEI 1*
2.18
(1.24-3.55)
–
–
4.92
(2.11-23.20)
2.58
(1.24-6.98)
0.71
(0.62-0.80)
May 8
(10/4-21/5)
May 14
(3/5-22/5)
BDEI 3*
2.00
(0.66-5.46)
1.85
(0.57-3.71)
3.15
(1.43-6.09)
5.92
(2.49-24.92)
2.71
(1.28-9.22)
0.71
(0.63-0.80)
May 5
(3/4-21/5)
May 13
(30/4-22/5)
Table 1 shows the results of the Bayesian birth-death analyses, including the times of origin and of the most recent common ancestor (MRCA). Under the constant birth-death-sampling model (BD1), we estimate an R0 of 1.65 (1.02-2.70), a sampling proportion of 65% (20-100%) and an infectious period of 6 days (2.84-18.84). There is no indication of a change in the reproductive number before mid June.
Since the BD model does not account for an incubation period, we also perform a simulation study in which we simulate an outbreak with incubation periods and analyse it under BD. This simulation shows that we can robustly estimate R0 under the BD model even without including an explicit incubation period, and that the estimate of the infectious period is roughly equal to the sum of incubation and infectious period in the simulations (Supplementary Table 1).
Allowing individuals to stay infectious upon sampling using the sampled ancestors model (BDsa) leads to very similar estimates of the epidemiological parameters. In fact, we only estimate two sampled ancestors in our dataset and the probability to become noninfectious upon sampling is large, 0.93 (0.71-1.00).
The epidemiological parameters are also estimated similarly under the BDSIR model, in which incidence can decline over time due to depletion of susceptible hosts. The initial number of susceptible individuals is estimated at 46000 (median) with large uncertainty (95% HPD, 380-534000). Estimating a similar R0 under a model that explicitly allows for the depletion of susceptible hosts over time suggests that the epidemic had not surpassed the exponential growth phase by mid June.
Using the BDEI model, which takes the incubation period into account, leads to slightly larger estimates of the basic reproductive number, 2.18 (1.24-3.55). There is a lot of uncertainty in our estimate of the incubation period of 5 days (2.11-23.20 days). Figure 3B shows that there is only little deviation of the posterior from the prior. The infectious period is estimated to be rather short, 2.58 days (1.24-6.98). Here, the posterior deviates a lot from the prior (Figure 3C). When we fix the incubation time to a shorter (2.3 days) or longer (5.6 days, as in Althaus (2014)23) period, we see a slight decrease or increase in the basic reproductive number, respectively. The times of origin (median May 8) and the MRCA (median May 14) show little variation.
Bayesian analysis in a coalescent framework
R0
Incubation
time (days)Infectious
time (days)Epidemic
originTree
MRCA
coalSEIR
1.90
(1.00-4.50)
6.23
(1.53-26.05)
8.66
(1.076-26.07)
May 5
(24/3-20/5)
May 14
(29/4-22/5)
(A) R0, (B) incubation period and (C) infectious period. We only show the posterior distributions for coalSEIR and BDEI with a constant reproductive number.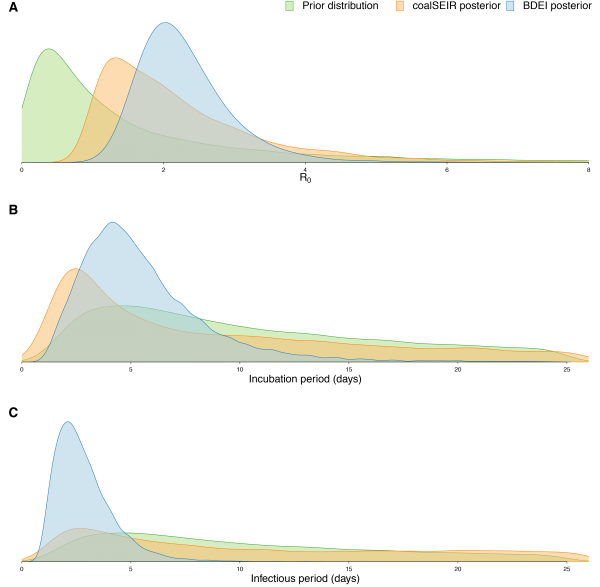
Fig. 3: Prior and posterior distributions of estimated parameters.
Epidemiological estimates obtained under the coalSEIR model were generally very similar to those obtained under the BDEI model, which was expected given that both approaches include an incubation period and account for uncertainty in the genealogy. Table 2 shows the estimated medians and 95% HPD intervals for the coalSEIR model parameters. While the credible intervals for R0 were wider under the coalSEIR than for the BDEI, R0 was estimated to be 1.90, just lower than under the BDEI model. Likewise, both methods returned a median epidemic origin time in the first weeks of May. We are not able to precisely estimate the duration of the exposed or infectious periods under the coalescent model, and our estimates appear to be largely informed by the prior, see Figure 3B and C.
Maximum Likelihood birth-death analyses based on fixed trees
R0/Re
initial
Re
middle
Re
recent
Incubation
time (days)Infectious
time (days)Sampling
probability
BD 1
1.34
(1.12-1.55)
–
–
–
4.45
(2.85-6.29)
0.7
(fixed)
BD 3
1.18
(0.54-1.72)
1.17
(0.87-1.59)
1.62
(1.37-1.90)
–
4.74
(3.26-6.99)
0.7
(fixed)
BDEI 1
1.45
(1.25-1.70)
–
–
2.29
(0.08-3.24)
2.07
(0.94-4.80)
0.7
(fixed)
BD 1
1.24
(1.08-1.37)
–
–
–
3.04
(2.16-4.32)
0.35
(fixed)
BD 3
1.02
(0.63-1.50)
1.10
(0.87-1.47)
1.44
(1.29-1.69)
–
3.28
(2.26-4.60)
0.35
(fixed)
BDEI 1
1.31
(1.19-1.45)
–
–
1.81
(1.22-2.58)
1.22
(0.61-2.22)
0.35
(fixed)
R0
(overall)
R0
(class 1)
R0
(class 2)
Fraction
class 1Infectious
time (days)Sampling
probability
BDss
1.57
(1.28-1.91)
2.63
(1.42-8.31)
0.84
(0.00-1.40)
0.45
(0.07-0.87)
5.16
(3.50-7.35)
0.7
(fixed)
Finally, we performed maximum likelihood parameter inference on fixed trees from Gire et al. (2014)12 . Because not all four parameters are jointly identifiable24, and because our Bayesian analysis confirmed previous estimates of the sampling probability, we fixed this parameter to 0.7 for times more recent than the oldest sample. Again, sampling probability was set to 0 prior to the oldest sample. To understand the sensitivity of our estimates with respect to this setting, we performed a second analysis fixing the sampling probability to 0.35.
For each of the 90 posterior trees, we obtained the maximum likelihood parameter estimates, see Table 3. Overall, assuming different fixed sampling probabilities did not significantly affect estimates. R0 was estimated slightly lower compared to the full Bayesian analyses above (medians 1.31-1.45). Again we did not find support for the reproductive number changing through time. A likelihood ratio test, comparing the results for three intervals for the reproductive number vs. a constant R0, does not support three intervals for the effective reproductive number over one interval (for a sampling probability of 0.7, 9 trees out of 90 supported three intervals for Re at the 95% level, and for a sampling probability of 0.35, 11 trees supported three intervals).
The upper bound for the number of days in the infected class across all analyses is 6.99 days. Thus, both full Bayesian and maximum likelihood methods suggest a time in exposed and infectious class that is lower than previous estimates.
As in the Bayesian analyses, when applying the BDEI method to the 90 Sierra Leone Ebola trees we obtain a slightly higher R0 when including the incubation period into the model.
When applying a birth-death model assuming two population groups with unique transmission rates, we observe that half of the population appears to have a large R0 (median 2.63, 95% HPD 1.42-8.31), and the other half does not appear to effectively spread the disease (R0 median 0.84, 95% HPD 0.00-1.40). However, likelihood ratio tests do not strongly support the structured model over the unstructured model.
Discussion
We used phylodynamic methods to estimate key epidemiological parameters of the current West African EBOV outbreak in Sierra Leone from sequencing data. Although we used a wide range of different models, we consistently recovered very similar estimates. In particular, we estimated the basic reproductive number of EBOV in Sierra Leone up to the time of the most recent sample (18 June 2014). The medians across the Bayesian methods were 1.65-2.18, with the most plausible model (BDEI) yielding a median estimate of 2.18 (95% HPD 1.24-3.55). We did not find any support for a reduction of the reproductive number prior to the most recent sample. Thus our results show that public health interventions during May and June were likely ineffective at reducing transmission in Sierra Leone. Furthermore, analyses suggest that there might be superspreaders among the infected population, however the significance of the population structure results should be reevaluated once larger datasets are available. We estimate expected incubation and infectious periods of 4.92 (2.11-23.20) and 2.58 (1.24-6.98) days. Using our birth-death methods, we confirm the previously estimated sampling proportion of 70%.
Our R0 estimates are within the range of estimates for previous outbreaks and other estimates for the current epidemic. For the 1995 EBOV Kikwit outbreak in the Democratic Republic of the Congo, R0 was estimated as 1.359±0.12825, 1.83±0.0626 or 2.7 (1.9-2.8)20. Towers et al. (2014)27 estimate an R0 of about 1.5 for the current West African EBOV epidemic, but only R0=1.2 (1.0,1.5) for the Sierra Leone epidemic, assuming incubation and infectious time periods of at most 7 days. Gomes et al. (2014)28 estimate an R0 of 1.8 (1.5-2.0) for the current West African EBOV outbreak while Althaus (2014)23 estimates an R0 of 2.53 (2.41-2.67) for the epidemic in Sierra Leone. Althaus (2014)23 further provides estimates of R0 for Guinea, 1.51 (1.50-1.52), and Liberia, 1.59 (1.57-1.60). Moreover he estimates that the Re in Sierra Leone has been declining since the onset of control measures and dropped below 1 during July. During the period from our samples his estimates of Re vary between 2.7 and 1.47. Nishiura and Chowell (2014)29 give estimates of Re in Sierra Leone and Liberia of between 1.4 and 1.7 during June and July, with Re in Guinea fluctuating erratically around 1 during the same period. Fisman et al. (2014)30 estimates values of R0 between 1.66 and 2.19 for the West African epidemic, however they estimate an R0 of 8.33 for the epidemic in Sierra Leone alone which is clearly outside our HPD intervals. The WHO Ebola Response Team estimated an R0 of 2.02 (1.79-2.26) for Sierra Leone from empirical data32. They also provide estimates for Guinea, 1.71 (1.44-2.01), and Liberia, 1.83 (1.72-1.94). These estimates are consistent with our estimates of R0.
We estimate short incubation and infectious periods with all of our birth-death methods. Estimates of the exposed and infectious periods for the 1995 EBOV Kikwit outbreak range from 5.3±0.23 and 5.61±0.19 days, respectively26, to 10.11±0.713 and 6.52±0.56 days25. However, for the 2000 Sudan Ebola virus (SUDV) outbreak in Uganda, Chowell et al. (2004)26 estimated the exposed and infectious periods to be 3.35±0.19 and 3.5±0.67 days. To the best of our knowledge the only estimates of the exposed and infectious periods for the current West African EBOV epidemic are by the WHO Ebola Response Team32, based on observational data. They estimate an incubation period of 9.0±8.1 days (median of 8 days) for 201 patients in Sierra Leone with single exposures. No overall infectious period is estimated, but instead the authors provide separate estimates for the infectious period based on disease outcome. From the onset of symptoms in patients sampled in Sierra Leone they estimate a period of 8.6±6.9 days (from 128 patients) until death, 17.2±6.2 days (from 70 patients) until hospital discharge and 4.6±5.1 days (from 395 patients) until hospitalisation.
Our HPD interval estimates for the incubation period are in line with other estimates, however our estimates for the infectious period are substantially shorter than estimates from the current epidemic32. Judging by the amount of variation in both the estimates from observational and genetic data we conclude that the incubation and infectious periods are highly variable and difficult to estimate accurately. However, we recover consistent estimates for the total time of infection (incubation + infectious periods), meaning there is a significant amount of information in the present dataset on the length of the infection. Sequencing data from more patients might help to get more confined credible intervals.
We see that a method accounting for an incubation period yields higher R0 estimates compared to a method assuming all infected individuals are infectious. As having an exposed class/incubation period will slow the initial growth of the epidemic, it is likely that estimates obtained under models that do not include the incubation period are lower to compensate for the slower growth rate. Thus it makes sense that R0 was estimated to be higher when the incubation period is included.
It is also noteworthy that both our BDEI and coalSEIR analyses converged on similar estimates for R0 and the epidemic origin. Thus our epidemiological estimates appear robust to the specific assumptions of these two models. Nonetheless, we do observe that our credible intervals for R0 and the exposed and infectious periods are considerably wider under the coalescent than the birth-death model. This may seem counterintuitive as the deterministic coalescent models used here ignore demographic stochasticity and should therefore underestimate the true level of uncertainty about the parameters. The confidence intervals being in fact wider under the coalescent may reflect the fact that the birth-death models are using information entering from the sampling times (while the coalescent conditions on sampling) to obtain more precise estimates of the epidemiological parameters.
Overall, we show that our inferences of the epidemiological dynamics of the current West African EBOV outbreak are robust to the model used and also consistent with estimates from previous outbreaks as well as other estimates of the current epidemic. Our hope is that more sequencing data from the epidemic will be made available in the immediate future. New data will allow us to estimate how the effective reproductive number has changed since June and allow us to estimate the incubation and infectious periods more reliably. Such estimates would be invaluable not only for evaluating the success of containment efforts, but also for planning future interventions.
Software availability
All Bayesian methods will become available within the BEAST213 add-on “phylodynamics” (https://github.com/BEAST2-Dev/phylodynamics) and are available directly from us prior to the official release. The maximum likelihood methods are available within our R packages TreeSim v2.131 and TreePar v3.116. We provide an R script specific to the Ebola analyses on our website (www.bsse.ethz.ch/cevo).
Competing Interests
The authors have declared that no competing interests exist.
Authorship
Acknowledgements
We thank Andrew Rambaut and Christian Althaus for helpful discussions and Andrew Rambaut for providing the Beast trees.Appendix 1
Supplementary Information
True
value Median
estimate Relative
error Relative
bias Relative
HPD width 95% HPD
accuracy
R0
1.5
1.561
0.136
0.041
0.764
97%
Incubation+infectious period
11.231
14.421
0.330
0.284
1.448
100%
Sampling probability
0.700
0.703
0.076
0.004
1.045
100%
Sampling change time
0.090
0.094
0.467
0.041
3.146
94%
(A) Incubation rate and (B) becoming-noninfectious rate (inverse of time). We only show the posterior distributions for coalSEIR and BDEI with a constant reproductive number.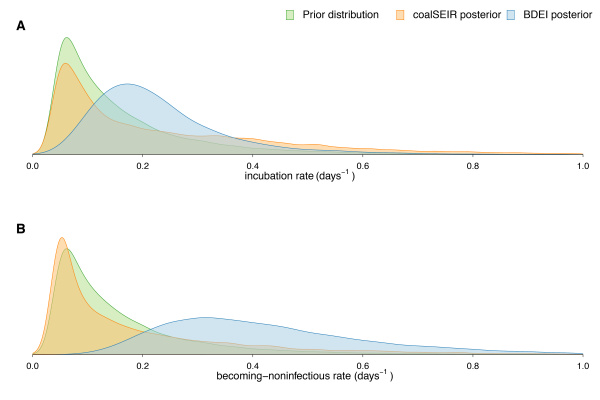
Fig. 1: (supplement) Prior and posterior distributions of estimated parameters.
References
- WHO Ebola response roadmap update, 3 October 2014.
Reference Link - Chan M. Ebola Virus Disease in West Africa - No Early End to the Outbreak. N Engl J Med. 2014 Aug 20. PubMed PMID:25140856.
- Briand S, Bertherat E, Cox P, Formenty P, Kieny MP, Myhre JK, Roth C, Shindo N, Dye C. The International Ebola Emergency. N Engl J Med. 2014 Aug 20. PubMed PMID:25140855.
- Bausch DG, Schwarz L. Outbreak of ebola virus disease in Guinea: where ecology meets economy. PLoS Negl Trop Dis. 2014 Jul;8(7):e3056. PubMed PMID:25079231.
- WHO Disease outbreak news: Ebola virus disease.
Reference Link - Ndambi R, Akamituna P, Bonnet MJ, Tukadila AM, Muyembe-Tamfum JJ, Colebunders R. Epidemiologic and clinical aspects of the Ebola virus epidemic in Mosango, Democratic Republic of the Congo, 1995. J Infect Dis. 1999 Feb;179 Suppl 1:S8-10. PubMed PMID:9988156.
- Dowell SF, Mukunu R, Ksiazek TG, Khan AS, Rollin PE, Peters CJ. Transmission of Ebola hemorrhagic fever: a study of risk factors in family members, Kikwit, Democratic Republic of the Congo, 1995. Commission de Lutte contre les Epidémies à Kikwit. J Infect Dis. 1999 Feb;179 Suppl 1:S87-91. PubMed PMID:9988169.
- Khan AS, Tshioko FK, Heymann DL, Le Guenno B, Nabeth P, Kerstiëns B, Fleerackers Y, Kilmarx PH, Rodier GR, Nkuku O, Rollin PE, Sanchez A, Zaki SR, Swanepoel R, Tomori O, Nichol ST, Peters CJ, Muyembe-Tamfum JJ, Ksiazek TG. The reemergence of Ebola hemorrhagic fever, Democratic Republic of the Congo, 1995. Commission de Lutte contre les Epidémies à Kikwit. J Infect Dis. 1999 Feb;179 Suppl 1:S76-86. PubMed PMID:9988168.
- Bwaka MA, Bonnet MJ, Calain P, Colebunders R, De Roo A, Guimard Y, Katwiki KR, Kibadi K, Kipasa MA, Kuvula KJ, Mapanda BB, Massamba M, Mupapa KD, Muyembe-Tamfum JJ, Ndaberey E, Peters CJ, Rollin PE, Van den Enden E, Van den Enden E. Ebola hemorrhagic fever in Kikwit, Democratic Republic of the Congo: clinical observations in 103 patients. J Infect Dis. 1999 Feb;179 Suppl 1:S1-7. PubMed PMID:9988155.
- Rodriguez LL, De Roo A, Guimard Y, Trappier SG, Sanchez A, Bressler D, Williams AJ, Rowe AK, Bertolli J, Khan AS, Ksiazek TG, Peters CJ, Nichol ST. Persistence and genetic stability of Ebola virus during the outbreak in Kikwit, Democratic Republic of the Congo, 1995. J Infect Dis. 1999 Feb;179 Suppl 1:S170-6. PubMed PMID:9988181.
- Rowe AK, Bertolli J, Khan AS, Mukunu R, Muyembe-Tamfum JJ, Bressler D, Williams AJ, Peters CJ, Rodriguez L, Feldmann H, Nichol ST, Rollin PE, Ksiazek TG. Clinical, virologic, and immunologic follow-up of convalescent Ebola hemorrhagic fever patients and their household contacts, Kikwit, Democratic Republic of the Congo. Commission de Lutte contre les Epidémies à Kikwit. J Infect Dis. 1999 Feb;179 Suppl 1:S28-35. PubMed PMID:9988162.
- Gire SK, Goba A, Andersen KG, Sealfon RS, Park DJ, Kanneh L, Jalloh S, Momoh M, Fullah M, Dudas G, Wohl S, Moses LM, Yozwiak NL, Winnicki S, Matranga CB, Malboeuf CM, Qu J, Gladden AD, Schaffner SF, Yang X, Jiang PP, Nekoui M, Colubri A, Coomber MR, Fonnie M, Moigboi A, Gbakie M, Kamara FK, Tucker V, Konuwa E, Saffa S, Sellu J, Jalloh AA, Kovoma A, Koninga J, Mustapha I, Kargbo K, Foday M, Yillah M, Kanneh F, Robert W, Massally JL, Chapman SB, Bochicchio J, Murphy C, Nusbaum C, Young S, Birren BW, Grant DS, Scheiffelin JS, Lander ES, Happi C, Gevao SM, Gnirke A, Rambaut A, Garry RF, Khan SH, Sabeti PC. Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak. Science. 2014 Sep 12;345(6202):1369-72. PubMed PMID:25214632.
- Bouckaert R, Heled J, Kühnert D, Vaughan T, Wu CH, Xie D, Suchard MA, Rambaut A, Drummond AJ. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput Biol. 2014 Apr;10(4):e1003537. PubMed PMID:24722319.
- Stadler T, Kouyos R, von Wyl V, Yerly S, Böni J, Bürgisser P, Klimkait T, Joos B, Rieder P, Xie D, Günthard HF, Drummond AJ, Bonhoeffer S. Estimating the basic reproductive number from viral sequence data. Mol Biol Evol. 2012 Jan;29(1):347-57. PubMed PMID:21890480.
- Volz EM. Complex population dynamics and the coalescent under neutrality. Genetics. 2012 Jan;190(1):187-201. PubMed PMID:22042576.
- Stadler T. Mammalian phylogeny reveals recent diversification rate shifts. Proc Natl Acad Sci U S A. 2011 Apr 12;108(15):6187-92. PubMed PMID:21444816.
- Stadler T, Kühnert D, Bonhoeffer S, Drummond AJ. Birth-death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc Natl Acad Sci U S A. 2013 Jan 2;110(1):228-33. PubMed PMID:23248286.
- Stadler T, Bonhoeffer S. Uncovering epidemiological dynamics in heterogeneous host populations using phylogenetic methods. Philos Trans R Soc Lond B Biol Sci. 2013 Mar 19;368(1614):20120198. PubMed PMID:23382421.
- Kühnert D, Stadler T, Vaughan TG, Drummand AJ. Phylodynamics meets phylogeography: A computational framework to quantify population structure from genomic data. (in preparation).
- Legrand J, Grais RF, Boelle PY, Valleron AJ, Flahault A. Understanding the dynamics of Ebola epidemics. Epidemiol Infect. 2007 May;135(4):610-21. PubMed PMID:16999875.
- Gavrushkina S, Welch D, Stadler T, Drummond AJ. Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration. (In press, PLoS Comp. Biol.)
Reference Link - Kühnert D, Stadler T, Vaughan TG, Drummond AJ. Simultaneous reconstruction of evolutionary history and epidemiological dynamics from viral sequences with the birth-death SIR model. J R Soc Interface. 2014 May 6;11(94):20131106. PubMed PMID:24573331.
- Althaus CL. Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. PLoS Currents Outbreaks. 2014 September 2.
- Stadler T. On incomplete sampling under birth-death models and connections to the sampling-based coalescent. J Theor Biol. 2009 Nov 7;261(1):58-66. PubMed PMID:19631666.
- Lekone PE, Finkenstädt BF. Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics. 2006 Dec;62(4):1170-7. PubMed PMID:17156292.
- Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J Theor Biol. 2004 Jul 7;229(1):119-26. PubMed PMID:15178190.
- Towers S, Patterson-Lomba O, Castillo-Chavez C. Temporal Variations in the Effective Reproduction Number of the 2014 West Africa Ebola Outbreak. PLoS Currents Outbreaks. 2014 Septemper 18.
- Gomes MFC, Pastore y Piontti A, Rossi L, Chao D, Longini I, Halloran ME, Vespignani A. Assessing the International Spreading Risk Associated with the 2014 West African Ebola Outbreak. PLOS Currents Outbreaks. 2014 September 2.
- Nishiura H, Chowell G. Early transmission dynamics of Ebola virus disease (EVD), West Africa, March to August 2014. Euro Surveill. 2014;19(36).
Reference Link - Fisman D, Khoo E, Tuite A. Early Epidemic Dynamics of the West African 2014 Ebola Outbreak: Estimates Derived with a Simple Two-Parameter Model. PLOS Currents Outbreaks. 2014 September 8.
- Stadler T. Simulating trees with a fixed number of extant species. Syst Biol. 2011 Oct;60(5):676-84. PubMed PMID:21482552.
- Ebola Virus Disease in West Africa - The First 9 Months of the Epidemic and Forward Projections. N Engl J Med. 2014 Sep 22. PubMed PMID:25244186.