Abstract
While the H1N1 pandemic is reaching high levels of influenza activity in the Northern Hemisphere, the attention focuses on the ability of national health systems to respond to the expected massive influx of additional patients. Given the limited capacity of health care providers and hospitals and the limited supplies of antibiotics, it is important to predict the potential demand on critical care to assist planning for the management of resources and plan for additional stockpiling. We develop a disease model that considers the development of influenza-associated complications and incorporate it into a global epidemic model to assess the expected surge in critical care demands due to viral and bacterial pneumonia. Based on the most recent estimates of complication rates, we predict the expected peak number of intensive care unit beds and the stockpile of antibiotic courses needed for the current pandemic wave. The effects of dynamic vaccination campaigns, and of variations of the relative proportion of bacterial co-infection in complications and different length of staying in the intensive care unit are explored.
Introduction
Official national reports from several countries in the Northern Hemisphere signal increasing influenza activity, as measured by the rise in the number of cases and patients requiring medical attention [1][2][3] . From the pandemic wave in the Southern Hemisphere [4] and the current activity [1][2][3] , a clearer picture of the severity of the disease has emerged in different geographic zones. Hospitalizations and number of cases requiring admission to intensive care unit (ICU) have been recorded, generating a picture of disease progression and illness severity requiring medical attention, hospitalization or critical care [4][5][6][7][8] . This data is also crucial for clinically assessing influenza-associated complications to update patient management recommendations [9][10][11][12][13][14][15] .
Given the limited availability of critical care facilities and medical resources, it is important to assess the expected potential burden on health services in order to face possible emergencies requiring highly specialized personnel and care units, for usually long and costly stays [16] . While a lot of work has been conducted on stockpiling and planning for deployment and distribution of antiviral drugs in case of an emerging influenza pandemic [17][18][19][20][21][22][23][24][25] , much less attention has been devoted to the role of bacterial pneumonia in pandemic planning, particularly in terms of stockpiling antimicrobial drugs [26][27] . Antibiotics are generally available through short supply chains able to fulfill average just-in-time requests. The pandemic wave is however expected to lead to a large increase in the usage pattern of antibiotics possibly relevant in the management of stockpiles not only during the peak phase but also during the decreasing trend of the epidemic activity. Based on the available knowledge of the severity of the disease and its associated complications, we present a computational study that explicitly considers the development of complications in order to estimate the predicted request of ICU resources and antibiotics needed to treat complications in several countries of the Northern Hemisphere, during the current Fall 2009 pandemic wave.
Methods
Baseline model
We use the global epidemic and mobility structured metapopulation model (GLEaM) [28][29] to provide pandemic scenarios and quantify the expected demand for critical care resources. The model is based on a meta-population approach [17][30][31][32][33][34][35][36][37][38][39] in which the world is divided into geographical regions defining a subpopulation network where connections among subpopulations represent the individual fluxes due to the transportation and mobility infrastructure. GLEaM integrates three different data layers [28][29] : (i) the population layer that integrates census areas for a total of 3362 subpopulations in 220 countries of the world; (ii) the human mobility layer that integrates both commuting flows collected from various sources in more than 30 countries and the airline traffic provided by IATA and OAG [28][29] ; (iii) the disease dynamics layer.
The model simulates short range mobility between subpopulations with a time scale separation approach that defines the effective force of infections in connected subpopulations [17][29][40][41] . The airline mobility from one subpopulation to another is modeled by an individual based stochastic procedure in which the number of passengers of each compartment traveling from a subpopulation j to a subpopulation l is an integer random variable defined by the actual data from the airline transportation database [17] . The infection dynamics takes place within each subpopulation. We adopt a SEIR -like model [42] in which we include vaccinated individuals and specific compartments for influenza associated complications. We also consider separate compartments for symptomatic traveling and not traveling, as well as asymptomatic individuals in each subpopulation. All transitions are modeled through binomial and multinomial processes to ensure the discrete and stochastic nature of the processes [17][29]. Asymptomatic individuals are considered as a fraction = 33% of the infectious individuals generated in the model and assumed to infect with a relative infectiousness of
= 50%[19][43]. Change in traveling behavior after the onset of symptoms is modeled with the probability
set to 50% that individuals would stop travelling when ill[19] (see Figure 1 for a detailed description of the compartmentalization). Initial conditions are defined by setting the start of the epidemic in La Gloria in Mexico on 18 February 2009[29][43][44]. In the model we use values of generation time interval and transmissibility according to the estimates of[29][45]. In particular, we use the reproductive number R 0 =1.75 with the generation interval set to 3.6 days (average latency period of 1.1 days and an average infectious period of 2.5 days). Those values are obtained by using the model to perform maximum likelihood analysis of the parameters against the actual chronology of newly infected countries as detailed in Ref.[29]. The method is computationally intensive as it involves a Monte Carlo generation of the distribution of arrival time of the infection in each country based on the analysis of 1 Million worldwide simulations of the pandemic evolution with the GLEaM model. It is important to remark that the best estimate of the reproductive number refers to the reference value that has to be rescaled by the seasonality scaling function. Seasonality is considered in the model by means of a sinusoidal forcing of the reproductive number, with a scaling factor ranging from αmin during Summer season to αmax during Winter season[33]. Here we consider αmax= 1.1 and αmin in the range 0.6 to 0.7, that is the best estimate obtained from the correlation analysis on the chronology of 93 countries seeded before June 18 in Ref.[29]. This seasonal scaling provides an effective reproductive number in the Northern hemisphere in the range 1.2 to 1.6 in the spring/fall months, in agreement with published estimates of the reproductive number. The best estimates of the model parameters provide predictions for the influenza activity peak in countries in the Northern Hemisphere in October/November in the baseline scenario[29], consistent with the influenza activity now being observed in surveillance reports[1][2][3]. In the following we will use the reference value αmin=0.6. A full discussion of the model’s limitations and of the sensitivity analysis of the model’s assumptions is reported in Ref.[29].
Vaccination
We model the administration of vaccines through a dynamic vaccination campaign with a uniform daily rate r v of distribution to the population in countries where doses are available, till their exhaustion. We explore two values for the daily distributions rate, r v =0.1% consistent with the current availability of doses and distribution in several countries, and r v =1% based on the distribution policies planned during Summer 2009 on the timing of vaccine development and testing [46] . We assume the administration of a single dose of vaccine, providing protection with a delay of 2 weeks. A full description of the vaccination implementation and sensitivity analysis is reported in Ref. [46] .
Influenza-associated complications
Following the most recent estimates of the severity of H1N1 pandemic, we assume a complication rate of 15% of clinical cases [7] , a hospitalization rate of 0.5% of clinical cases [6] , and an ICU admission rate of 15% of hospitalized patients [3] . We model influenza-related pneumonia as a complication associated to influenza infection, considering two main types of pneumonia – primary viral pneumonia and secondary bacterial pneumonia. While bacterial coinfection was shown to be the predominant cause of death in previous influenza pandemics [47] , its presence in the severe cases analyzed since the start of the outbreak range from almost no evidence in the early reviews [9][10][11] , to about 10% [13] , 33% or larger proportions [14][15] of the cases presenting influenza-associated complications. These fluctuations in the role of bacterial pneumonia might be due to the difficulty of testing for specific bacterial diagnosis, or to the use of antibiotics prior to routine clinical tests. Given the uncertainty on the cause of pneumonia at this stage of the epidemic evolution, we assume a proportion of bacterial pneumonia in cases showing complications in the range of a= 33-50%, with a sensitivity exploring a 10% proportion. Under pandemic conditions, it is assumed that very small differences will be implemented in the management and treatment of the patients with either types of pneumonia, as the diagnosis of influenza-associated complications will be mostly based on clinical findings and most prescribing will be empirical, based on both antibacterial therapy and antiviral medications [48] . Multiple subsequent stages of pneumonia course are modeled according to the CURB-65 classification score [49] as reported in Table 1, and different progressions are assumed to take into account both viral and bacterial pneumonia (see Figure 1). It is also worth remarking that the model does not consider social structure in the subpopulations, therefore the effect of prioritized distribution of vaccines to individuals belonging to risk groups in reducing the number of hospitalizations and deaths is not considered in the present study. These assumptions represent a necessary trade-off for the computational efficiency of the model that allows to perform parameter estimations fitting the worldwide pattern of the pandemic [29] , explore several scenarios under different conditions, and perform sensitivity analysis on the assumptions. Once the disease parameters and initial conditions are defined, GLEaM generates in-silico epidemics for which we can gather information such as incidence and prevalence of all stages considered in the compartmentalization, for each subpopulation in the world and with a time resolution of one day. All results shown in the following sections are obtained from the statistics based on at least 2,000 stochastic runs of the model.
Results and Discussion
Based on the available knowledge of complication, hospitalization and ICU rates, and the relative proportion of bacterial vs. viral pneumonia, the simulation results allow the measure of the predicted need of beds in intensive care units, and provide estimates of the corresponding courses of antibiotics needed. Figure 2 shows the time evolution of the predicted prevalence of ICU occupancy for a given set of countries. In the baseline case, when no intervention is implemented, the ICU prevalence peak ranges between approximately 5 and 7 ICU beds per 100,000 people. These values are well below the national average capacity of some countries, such as e.g. the United States with a total of about 20 ICU beds per 100,000 [50] and Germany with an average of approximately 28 ICU beds per 100,000 [51] . The predicted need is slightly lowered if a 0.1% dynamic vaccination is considered, and would be reduced to values in the range of 3.6 to 4.8 ICU beds per 100,000 if we assume r v =1%, below the national average number of ICU beds of many European countries [16] . While the predicted ICU beds needs are averaged at the country level to conform with the capacity data, it is however important to note that the impact and the potential occurrence of critical situations strongly depends on the geographic distribution of the critical care resources, with areas that might have access to a larger number of intensive care units than others (see for example Ref. [52] ). Moreover, a direct comparison between the simulated demand and critical care availability is made difficult by the lack of a standard definition for intensive care unit beds, and the large variations observed in both numbers of beds and volume of admission between countries in North America and Western Europe [16] .
The results shown in Figure 2 are based on an average ICU length of staying equal to L ICU =7 days. Since there is a large variation in this parameter, with cohort studies showing median duration of 7 days and interquartile range up to approximately 2 weeks [15] , we also explored the effect of considering longer lengths of staying, L ICU =10 and L ICU =14 days. The longer bed occupancy would inevitably lead to an increase in the need of ICU beds at peak, in the range of approximately 9 to 12 per 100,000 persons in the case of 14 days of average ICU duration (see Table 2).
Table 3 reports the number of antibiotics courses needed daily at the peak of the requests, and the total size predicted to be used at the end of the pandemic wave, based on the empirical guidelines of the British Thoracic Society [49][53] and broken down by the stage of severity of pneumonia. A single course of antibiotics is defined as the combination of antimicrobial drugs considered in the treatment regimen for the suggested duration (see Table 1). In the case of non severe pneumonia, the predicted need for antibiotics at peak usage is in the range of [150-230] courses per 100,000 with variations depending on the country under study, under the assumption that no intervention is considered. The total size of antibiotics courses predicted to be used in the current Fall 2009 pandemic is in the range of [6,337-7,149] per 100,000, which needs to be compared with the available stockpiles of antibiotics courses to cover high-risk groups. Many countries however do not possess nation-wide antibiotic supplies, and the estimates contained in Table 3 can therefore be considered as guidelines to assess the expected needs during the remaining evolution of the pandemic wave with respect to the present usage pattern and available resources.
Along with anecdotal reports indicating ICUs being overwhelmed by the sudden surge of H1N1 cases with severe complications [54] , studies on the Winter experience in the Southern Hemisphere during the H1N1 pandemic wave confirm a substantial impact on ICUs, with the maximum number of ICU beds occupied by region in Australia and New Zealand ranging between 0.63 and 1.1 per 100,000 inhabitants [15] . These values are smaller than the ICU demands predicted for the Fall wave in the Northern Hemisphere. It is important to note, however, that the used model does not take into account the population structure (age dependent attack rates), risk groups and prior immunity thus likely overestimating the global attack rate of the pandemic. Furthermore we do not include in the model mitigation factors (e.g. social distancing, targeted school closures, etc.) that might have contributed to the reduction of the overall burden on the critical care facilities in the Southern Hemisphere; a similar reduction on burden could also be seen in the Northern Hemisphere.
Accurate descriptions of expected scenarios are important to define and quantify the expected increase in the needs for healthcare infrastructure and medical resources. With the uncertainties on the evolution of the current pandemic wave decreasing, these estimates can be used to better plan for potential additional resources that might be needed in a short time, both at the peak time and after the peak activity has been reached. A full comparison and understanding of similarities and differences of the Winter pandemic waves in the two Hemispheres will then be crucial for understanding the impact of H1N1 pandemic on the population and on the health care infrastructure in different settings.
Competing interests
AV is consulting and has a research agreement with Abbott for the modeling of H1N1 diffusion. The other authors have declared that no competing interests exist.
Authors’ contributions
DB, ACS, CC, A-JV contributed to conceiving and designing the study, and helped to draft the manuscript. DB performed numerical simulations and statistical analysis, and contributed to the data integration. HH, BG, PB, CP, JJR, DP, NP, MT, WVdB contributed to data tracking and integration, and to the estimation of disease parameters. AV and VC conceived, designed and coordinated the study, contributed to the analysis and methods development and drafted the manuscript. All authors read and approved the final manuscript.
Correspondence
Correspondence to [email protected] or [email protected]
Acknowledgments
The authors thank IATA and OAG for providing their databases.
Funding
This work has been partially funded by the NIH R21-DA024259 award, the Lilly Endowment grant 2008 1639-000, and the DTRA-1-0910039 award to AV; the EC-ICT contract no. 231807 (EPIWORK), and the EC-FET contract no. 233847 (DYNANETS) to AV, VC; the ERC Ideas contract n.ERC-2007-Stg204863 (EPIFOR) to VC; the Natural Environment Research Council – Knowledge Transfer Initiative (PREPARE) contract no. NE/F009216/1 to ACS.
Figures
A susceptible individual interacting with an infectious person may contract the illness and enter the latent compartment where he is infected but not yet infectious. At the end of the latency period, each latent individual becomes infectious entering the symptomatic compartment with probability (1-p a ) or becoming asymptomatic with probability p a . Asymptomatic individuals infect with a reduced transmission rate. A fraction (1-p t ) of the symptomatic individuals would stop traveling when ill. A full description of the parameter values is reported in Ref. [29] . If vaccines are available, a fraction equal to r v of the susceptible population enters the susceptible vaccinated compartment each day. A similar progression to the baseline compartmentalization is considered if infection occurs (see Ref. [46] ). The model assumes that infectious individuals might develop complications with a rapid progression to severe conditions requiring hospitalization or ICU admission (i.e. second and third stage of the complications tree, respectively), or home treatment (i.e. first stage) with pneumonia symptoms appearing during the early convalescent period of the influenza infection [49] . The compartments ‘hospital ward 1’ and ‘hospital ward 2’ refer to different lengths of staying of the patient in the hospital ward (see Table 1), depending on subsequent worsening of symptoms or direct recovery, respectively. Progressions from one stage to the others is modeled according to the average length of staying in each compartment as obtained from clinical studies [13][15] (see also Table 1) and based on the available estimates of complication, hospitalization and ICU admission rates [3][6][7] .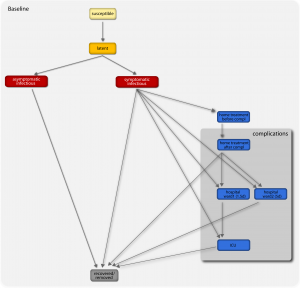
Fig. 1: Diagram flow of the transmission model.
ICU occupancy measures the predicted need of ICU beds per 100,000 persons. Results for the United States, France, Germany, and Spain are shown. The three profiles per each country refer to the predicted ICU occupancy in the baseline case when no intervention is implemented, and in case dynamic vaccination campaigns with distribution rates r v =0.1% and r v =1% are considered. Solid curves correspond to the median profiles and the shaded areas to the 95% reference range obtained from 2,000 stochastic simulations. The average ICU length of staying is assumed equal to 7 days [15] .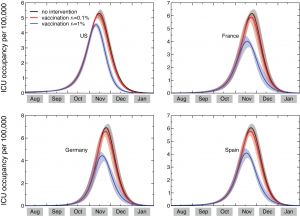
Fig. 2: Time evolution of the ICU occupancy in a set of countries
Tables
| Severity of complications | Assessment | Recommendedaction /compartmentalization | Average duration |
| non-severe pneumonia | CURB-65=0-2 | home treatment or supervised outpatient treatment | 3.5 days [9] |
| severepneumonia | CURB-65=3or presence of bilateral lung infiltrates on chest x ray | hospital ward | 1.5 days to ICU admission (hospital ward 1), 5 days to recovery (hospital ward 2) [13] |
| CURB-65=4-5or bilateral chest x ray changes |
ICU |
7, 10, 14 days [13][15] |
Table 1: Severity assessment, recommended action, and estimated durations assumed in the model. We refer to CURB-65 score as the method used to determine the management of influenza-related complications in patients admitted to hospital [49] . CURB-65 score is calculated by assigning one point for each of the following: Confusion (mental test score of =8, or new disorientation in person, place or time),Urea >7 mmol/l, Respiratory rate =30/min, Blood pressure (SBP<90 mmHg or DBP=60 mmHg), Age =65 years. Three subsequent stages are defined to model complications, based on the recommended action. Patients with bilateral lung infiltrates on chest radiography consistent with viral pneumonia are assumed to be managed as severe pneumonia, regardless of CURB-65 score [49] . The preferred empirical antibiotic regimens for treatment of patients in each stage are based on the guidelines issued by the British Thoracic Society [49][53] . Patients in home treatment and hospital ward are assumed to take co-amoxiclav 625mg tds PO or doxycycline 200mg stat and 100mg od PO for 7 days, and patients in ICU are assumed to take co-amoxiclav 1.2g tds IV or cefuroxime 1.5g tds IV or cefotaxime 1g tds IV plus Macrolide (erythromycin 500mg qds IV or clarithromycin 500mg bd IV) for 10 days. All patients at all stages of severity of complications are also expected to receive antivirals, with a dosage of 2 tablets per day.
| ICU occupancy at peak (per 100,000) | |||||||||
| Country | Baseline | Vaccination campaigns | |||||||
| 0.1% | 1% | ||||||||
| 7 days | 10 days | 14 days | 7 days | 10 days | 14 days | 7 days | 10 days | 14 days | |
| US | [5.0-5.6] | [6.8-7.5] | [8.7-9.7] | [5.0-5.5] | [6.7-7.3] | [8.6-9.4] | [4.5-4.6] | [5.9-6.2] | [7.6-7.9] |
| UK | [5.7-6.5] | [7.6-8.6] | [9.9-11.0] | [5.5-6.2] | [7.4-8.2] | [9.6-10.5] | [3.9-4.6] | [5.2-6.1] | [6.7-7.7] |
| Canada | [5.0-5.7] | [6.7-7.6] | [8.7-9.9] | [4.8-5.5] | [6.5-7.3] | [8.5-9.5] | [3.8-4.4] | [5.1-5.8] | [6.5-7.3] |
| France | [5.9-6.6] | [7.9-8.7] | [10.2-11.2] | [5.7-6.2] | [7.6-8.3] | [9.8-10.6] | [3.6-4.4] | [4.9-5.9] | [6.3-7.4] |
| Italy | [6.5-7.1] | [8.6-9.4] | [11.0-12.0] | [6.2-6.7] | [8.2-8.9] | [10.5-11.3] | [3.6-4.5] | [4.8-5.9] | [6.1-7.4] |
| Spain | [5.8-6.4] | [7.8-8.6] | [10.0-11.0] | [5.6-6.1] | [7.5-8.2] | [9.6-10.5] | [3.8-4.5] | [5.1-5.9] | [6.5-7.5] |
| Germany | [6.6-7.3] | [8.8-9.7] | [11.2-12.2] | [6.4-7.0] | [8.5-9.2] | [10.8-11.6] | [4.0-4.8] | [5.4-6.4] | [6.8-8.0] |
Table 2: Predicted need of ICU beds in the baseline case scenario and in the case of vaccination campaigns. The 95% reference range (RR) of the daily number of occupied ICU beds per 100,000 is reported at its peak for several countries in the Northern Hemisphere.
| Antibiotic usage – baseline | ||||||
| Country | Daily administered AB courses at peak (per 100,000) | Total administered AB courses at the end of pandemic wave (per 100,000) | ||||
| Pneumonia stage I | Pneumonia stage II | Pneumonia stage III | Pneumonia stage I | Pneumonia stage II | Pneumonia stage III | |
| US | [152-171] | [4.4-4.9] | [0.8-0.9] | [6,196-6,455] | [183-191] | [31.7-33.0] |
| UK | [176-197] | [5.1-5.8] | [0.9-1.1] | [6,529-6,845] | [193-203] | [33.3-35.1] |
| Canada | [150-170] | [4.4-5.0] | [0.8-1.0] | [6,508-6,755] | [192-200] | [33.0-34.8] |
| France | [184-201] | [5.3-5.9] | [1.0-1.1] | [6,611-6,906] | [195-204] | [33.7-35.4] |
| Italy | [202-221] | [5.8-6.4] | [1.1-1.2] | [6,758-6,981] | [200-206] | [34.4-35.8] |
| Spain | [178-195] | [5.2-5.7] | [0.9-1.1] | [6,584-6,815] | [194-202] | [33.4-35.1] |
| Germany | [208-230] | [5.9-6.6] | [1.1-1.2] | [6,739-6,990] | [199-207] | [34.4-35.8] |
| Antibiotic usage – vaccination with r v=0.1% | ||||||
| Country | Daily administered AB courses at peak (per 100,000) | Total administered AB courses at the end of pandemic wave (per 100,000) | ||||
| Pneumonia stage I | Pneumonia stage II | Pneumonia stage III | Pneumonia stage I | Pneumonia stage II | Pneumonia stage III | |
| US | [151-166] | [4.4-4.8] | [0.8-0.9] | [6,005-6,220] | [177-184] | [30.7-31.9] |
| UK | [170-186] | [4.9-5.4] | [0.9-1.0] | [6,297-6,540] | [186-193] | [32.1-33.6] |
| Canada | [147-164] | [4.3-4.9] | [0.8-0.9] | [6,278-6,457] | [185-191] | [31.8-33.3] |
| France | [176-188] | [5.1-5.5] | [0.9-1.0] | [6,357-6,585] | [188-195] | [32.3-33.8] |
| Italy | [191-206] | [5.5-6.0] | [1.0-1.1] | [6,481-6,633] | [191-196] | [32.9-34.1] |
| Spain | [171-185] | [5.0-5.4] | [0.9-1.0] | [6,335-6,511] | [187-193] | [32.1-33.6] |
| Germany | [200-216] | [5.7-6.2] | [1.0-1.2] | [6,476-6,654] | [191-197] | [33.0-34.2] |
| Antibiotic usage – vaccination with r v=1% | ||||||
| Country | Daily administered AB courses at peak (per 100,000) | Total administered AB courses at the end of pandemic (per 100,000) | ||||
| Pneumonia stages I | Pneumonia stage II | Pneumonia stage III | Pneumonia stages I | Pneumonia stage II | Pneumonia stage III | |
| US | [140-144] | [4.0-4.1] | [0.7-0.8] | [4,801-4,862] | [142-144] | [24.5-25.0] |
| UK | [120-140] | [3.5-4.1] | [0.6-0.8] | [4,452-4,762] | [131-141] | [22.7-24.5] |
| Canada | [121-133] | [3.5-3.9] | [0.6-0.8] | [4,517-4,732] | [133-140] | [22.9-24.4] |
| France | [110-136] | [3.2-4.0] | [0.6-0.7] | [4,390-4,682] | [130-139] | [22.4-24.0] |
| Italy | [110-136] | [3.2-4.0] | [0.6-0.7] | [4,230-4,539] | [125-134] | [21.5-23.3] |
| Spain | [116-137] | [3.4-4.0] | [0.6-0.8] | [4,429-4,652] | [131-137] | [22.5-24.0] |
| Germany | [126-150] | [3.6-4.3] | [0.7-0.8] | [4,311-4,655] | [127-138] | [22.0-23.9] |
Table 3: Predicted usage pattern of antibiotics in the baseline case scenario and in the case of vaccination campaigns. The 95% RR of the daily number of administered antibiotics courses per 100,000 at its peak is reported, along with the total amount predicted to be administered by the end of the pandemic wave. Results are shown for several countries in the Northern Hemisphere, broken down for different stages of influenza-associated complications. Pneumonia stages I, II and III corresponds to home-treatment (or supervised outpatient treatment), hospital wards and ICU, respectively (see Figure 1 and Table 1).
References
- World Health Organization, Pandemic (H1N1) 2009 – update 75
Reference Link - Centers for Disease Control and Prevention, 2009 H1N1 Flu Situation Update (November 23, 2009)
Reference Link - European Centre for Disease Control and Prevention, Pandemic (H1N1) 2009 Daily Update (November 23, 2009), European Centre for Disease Control and Prevention, Pandemic (H1N1) 2009 Daily Update (November 23, 2009)
- World Health Organization, Pandemic (H1N1) 2009 – Preparing for the second wave: lessons from current outbreaks (August 28, 2009)
Reference Link - Lipsitch M et al, The severity of pandemic H1N1 influenza in the United States, April – July 2009, 2009 RRN1042.
- Reed C et al, Estimates of the prevalence of pandemic (H1N1) 2009, United States, April-July 2009. Emerg Infect Dis (2009) DOI: 10.3201/eid1512.091413.
- UK Department of Health. Swine Flu: UK planning assumptions. Issued 3 September, (2009)
Reference Link - Flahault A. First estimation of direct H1N1pdm virulence: From reported non consolidated data from Mauritius and New Caledonia. PLoS Currents Influenza. 2009 Sep 23:RRN1010.
- Perez-Padilla R, de la Rosa-Zamboni D, Ponce de Leon S, et al. Pneumonia and Respiratory Failure from Swine-Origin Influenza A (H1N1) in Mexico. New Engl J Med 361:680-689 (2009).
- CDC. Hospitalized patients with novel influenza A (H1N1) virus infection---California, April--May, 2009. MMWR 2009;58:536--41.
- CDC. Intensive-care patients with severe novel influenza A (H1N1) virus infection---Michigan, June 2009. MMWR 2009;58:749--52.
- Kaufman MA, et al. Life-threatening respiratory failure from H1N1 influenza 09 (human swine influenza). Medical Journal of Australia, 55030578 (2009).
- Rello J et al, Intensive care unit with severe respiratory failure caused by influenza A(H1N1)v in Spain. Critical Care 13:R148 (2009).
- CDC. Bacterial Coinfections in Lung Tissue Specimens from Fatal Cases of 2009 Pandemic Influenza A (H1N1) --- United States, May--August 2009. MMWR 2009;58:1-4.
- The ANZIC Influenza Investigators. Critical Care Services and 2009 H1N1 Influenza in Australia and New Zealand. New Engl J Med 361, 1925-1934 (2009).
- Wunsch H et al. Variation in critical care services across North America and Western Europe. Crit Care Med 2008 36, 2787.
- Colizza V, Barrat A, Barthelemy M, Valleron A-J, Vespignani A: Modeling the Worldwide spread of pandemic influenza: baseline case and containment interventions. PloS Medicine 2007, 4: e13.
- Flahault A, Vergu E, Coudeville L, Grais R: Strategies for containing a global influenza pandemic. Vaccine 2006, 24: 6751-6755.
- Longini IM, Halloran ME, Nizam A, Yang Y: Containing pandemic influenza with antiviral agents. Am J Epidemiol (2004) 159: 623–633.
- Gani R, Hughes H, Fleming D, Griffin T, Medlock J, Leach S. Potential impact of antiviral drug use during influenza pandemic. Emerg Infect Dis 2005, 11:1355-1362.
- Ferguson NM, Cummings DA, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, Burke DS: Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 2005, 437:209-214.
- Germann TC, Kadau K, Longini IM, Macken CA: Mitigation strategies for pandemic influenza in the United States. Proc Natl Acad Sci USA 2006, 103:5935-5940.
- Arinaminpathy N, McLean AR: Antiviral treatment for the control of pandemic influenza: some logistical constraints. J R Soc Interface 2008, 5:545-553.
- Wu JT, Riley S, Fraser C, Leung GM: Reducing the impact of the next influenza pandemic using household-based public health interventions. PLoS Med 2006, 3:e361.
- Merler S, Ajelli M, Rizzo C. Age-prioritized use of antivirals during an influenza pandemic. BMC Infectious Diseases, 9:117, 2009.
- Gupta RK, George R, Nguyen-Van-Tam JS. Bacterial pneumonia and pandemic influenza planning. Emerg Infect Dis 14, 1187 (2008).
- Bonten MJM. Antibiotics in pandemic flu. BMJ 332:248-249 (2006).
- Balcan D, Colizza V, Gonçalves B, Hu H, Ramasco JJ, Vespignani A: Multiscale mobility networks and the large scale spreading of infectious diseases. Proc Natl Acad Sci USA (2009) in press. Preprint available at: arXiv:0907.3304.
- Balcan D, Hu H, Goncalves B, Bajardi P, Poletto C, Ramasco JJ, Paolotti D, Perra N, Tizzoni M, Van den Broeck W, Colizza V, Vespignani A. Seasonal transmission potential and activity peaks of the new influenza A(H1N1): a Monte Carlo likelihood analysis based on human mobility. BMC Medicine 7, 45 (2009).
- Rvachev LA, Longini IM: A mathematical model for the global spread of influenza. Mathematical Biosciences 1985, 75:3–22.
- Grais RF, Hugh Ellis J, Glass GE: Assessing the impact of airline travel on the geographic spread of pandemic influenza. Eur. J. Epidemiol. 2003, 18:1065–1072.
- Hufnagel L, Brockmann D, Geisel T: Forecast and control of epidemics in a globalized world. Proc. Natl. Acad. Sci. (USA) 2004, 101:15124–15129.
- Cooper BS, Pitman RJ, Edmunds WJ, Gay N: Delaying the international spread of pandemic influenza. PloS Medicine 2006, 3:e12.
- Epstein JM, Goedecke DM, Yu F, Morris RJ, Wagener DK, Bobashev GV: Controlling Pandemic Flu: The Value of International Air Travel Restrictions. PLoS ONE 2007, 2: e401.
- Viboud C, Bjornstad O, Smith DL, Simonsen L, Miller MA, Grenfell BT: Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 2006, 312:447–451.
- Flahault A, Valleron A-J: A method for assessing the global spread of HIV-1 infection based on air travel. Math. Popul. Stud. 1991, 3:1–11.
- Colizza V, Barrat A, Barthélemy M, Vespignani A: The role of airline transportation network in the prediction and predictability of global epidemics. Proc. Natl. Acad. Sci. (USA) 2006, 103:2015–2020.
- Colizza V, Barrat A, Barthélemy M, Vespignani A: Predictability and epidemic pathways in global outbreaks of infectious diseases: the SARS case study. BMC Med 2007, 5:34.
- Coburn BJ, Bradley G Wagner BG, Blower S: Modeling influenza epidemics and pandemics: insights into the future of swine flu (H1N1), BMC Medicine 2009, 7:30.
- Keeling MJ, Rohani P: Estimating spatial coupling in epidemiological systems: a mechanistic approach. Ecology Letters 2002, 5:20–29.
- Sattenspiel L, Dietz K: A structured epidemic model incorporating geographic mobility among regions. Math. Biosci. 1995, 128:71–91.
- Anderson RM, May RM: Infectious Diseases in Humans. Oxford Univ. Press, Oxford 1992.
- Fraser C et al: Pandemic potential of a strain of influenza A(H1N1): early findings. Science 2009, 324: 1557-1561.
- Brote de infeccion respiratoria aguda en La Gloria, Municipio de Perote, Mexico. Secretaria de Salud, Mexico
Reference Link - Yang Y et al., The transmissibility and control of pandemic influenza A(H1N1) virus, Science 326, 729 – 733.
- Bajardi P, Poletto C, Balcan D, Hu H, Goncalves B, Ramasco JJ, Paolotti D, Perra N, Tizzoni M, Van den Broeck W, Colizza V, Vespignani A. Modeling vaccination campaigns and the Fall/Winter 2009 activity of the new A(H1N1) influenza in the Northern Hemisphere. Emerging Health Threats Journal 2009, 2:e11.
- Morens DM, Taubenberger, Fauci AS. Predominant role of bacterial pneumonia as a cause of death in pandemic influenza: implications for pandemic influenza preparedness. J Infect Dis 2008, 198:962-970.
- World Health Organization. Clinical management of human infection with pandemic (H1N1) 2009: revised guidance, November 2009
Reference Link - Lim WS. Pandemic flu: clinical management of patients with an influenza-like illness during an influenza pandemic. Thorax 62, 1-46 (2007).
- Society of Critical Care Medicine, Critical Care Statistics in the United States 2006
Reference Link - The Information System of the Federal Health Monitoring
Reference Link - Ercole A, Taylor BL, Rhodes A, Menon DK. Modelling the impact of an influenza A/H1N1 pandemic on critical care demand from early pathogenicity data: the case for sentinel reporting. Anaesthesia 64, 937-941 (2009).
- British Thoracic Society.
Reference Link - Bita N. No bed for swine flu man on life support. The Australian (2009).
Leave a Comment
You must be logged in to post a comment.