Abstract
We developed an agent-based model to investigate the epidemic dynamics of Ebola virus disease (EVD) in Liberia and Sierra Leone from May 27 to December 21, 2014. The dynamics of the agent-based simulator evolve on small-world transmission networks of sizes equal to the population of each country, with adjustable densities to account for the effects of public health intervention policies and individual behavioral responses to the evolving epidemic. Based on time series of the official case counts from the World Health Organization (WHO), we provide estimates for key epidemiological variables by employing the so-called Equation-Free approach. The underlying transmission networks were characterized by rather random structures in the two countries with densities decreasing by ~19% from the early (May 27-early August) to the last period (mid October-December 21). Our estimates for the values of key epidemiological variables, such as the mean time to death, recovery and the case fatality rate, are very close to the ones reported by the WHO Ebola response team during the early period of the epidemic (until September 14) that were calculated based on clinical data. Specifically, regarding the effective reproductive number Re, our analysis suggests that until mid October, Re was above 2.3 in both countries; from mid October to December 21, Re dropped well below unity in Liberia, indicating a saturation of the epidemic, while in Sierra Leone it was around 1.9, indicating an ongoing epidemic. Accordingly, a ten-week projection from December 21 estimated that the epidemic will fade out in Liberia in early March; in contrast, our results flashed a note of caution for Sierra Leone since the cumulative number of cases could reach as high as 18,000, and the number of deaths might exceed 5,000, by early March 2015. However, by processing the reported data of the very last period (December 21, 2014-January 18, 2015), we obtained more optimistic estimates indicative of a remission of the epidemic in Sierra Leone, as reflected by the derived Re (~0.82, 95% CI: 0.81-0.83).
Funding Statement
The authors have declared that no competing interests exist. No external funding was received for this work.INTRODUCTION
An outbreak of a communicable disease associated with a high fatality rate in the rural forest communities of Guinea in December 2013 has spiraled into an epidemic that is ravaging West Africa and evoking fear around the globe.1 Ebola virus (EBOV, formerly Zaire ebolavirus), one of the five species of the genusEbolavirus, has been identified as the causative agent of this unprecedented epidemic, in terms of initial geographic occurrence, magnitude, complexity and persistence.1,2 EBOV was also involved in previous outbreaks in remote regions of Central Africa, with the largest, in the Democratic Republic of Congo (DR Congo, formerly Zaire) in 1976, accounting for merely 318 cases, including 280 deaths.3 The current Ebola Virus Disease (EVD) epidemic has plagued major urban centers in West Africa, in some of the most impoverished and logistically challenged countries of the world. According to the World Health Organization (WHO), as of January 12, 2015, 8,362 and 10,150 cases, including 3,556 and 3,067 deaths, respectively, have been officially reported in Liberia and Sierra Leone, the countries mostly afflicted along with Guinea, while the concern of further international spread has not ceased.4
Mathematical models are instrumental in providing guidance as to the future projections of such important ongoing public health crises, and in assessing the potential impact interventions might have towards transmission control.5 Models can be distinguished to four different categories associated with increasing levels of epidemiological realism and, consequently, with increasing difficulty in the systematic analysis:5,6 (i) Deterministic models in the form of differential or (integro)-partial differential equations are “continuum models” describing the coarse-grained dynamics of epidemics at the population level; (ii) relaxing the hypothesis of continuum models about infinite population, stochastic models incorporate stochastic parameters and variables; (iii) individual-based models with “memory” import the uniqueness of the individual behavior in a general population while relaxing the hypothesis of stochastic ones about structural uniformity in their interactions; (iv) the most complex, dynamic “social” network-based or agent-based models emphasize the heterogeneous nature and potential for delayed effects of the interactions between individuals.
Both deterministic and stochastic SEIR (susceptible-exposed-infectious-recovered) dynamic models have been used to study the 1995 and 2000 Ebola outbreaks in DR Congo and Uganda, which were caused by the Zaire and Sudan virus strains, correspondingly.7,8 Legrand et al.9, in particular, analyzed data from these two epidemics with a sixth-order stochastic compartmental model that incorporated explicitly the settings of transmission in the community, in the hospital and during traditional burial ceremonies. To explore the impact of control interventions, they simulated various epidemic scenarios and found that the rapid institution of control measures was a key parameter, whilst increasing hospitalization rate reduced the predicted epidemic size for both epidemic profiles.
For the current Ebola outbreak in West Africa, Rivers et al.10 utilized the model proposed by Legrand9 to approximate and forecast the evolution of the spread in Liberia and Sierra Leone. Their model forecasted a continuously increasing epidemic until December 31, 2014, with medians of 117,877 and 30,611 cases for Liberia and Sierra Leone, respectively. Kiskowski11 combined a stochastic SEIR model with a three-scale community network model representing contacts between households and local communities, to demonstrate that the different regional trends of the early growth dynamics of the 2014 EBOV epidemic in Guinea, Sierra Leone and Liberia might be explained by disparate local community mixing rates. A compartmental stochastic, individual-based model employed by Gomes et al.12 to approximate the dynamics of the Ebola outbreak worldwide at an early period of the outbreak, estimated a rapid increase of the cases in African countries, and a potential international threat on a longer time-scale.
Althaus13 used a deterministic SEIR dynamic model to estimate two vital epidemiological parameters for any infection, describing the spread of EBOV in West African countries, in this case: the basic and the effective reproduction numbers, R0 and Re, correspondingly, i.e., the number of secondary cases generated by an infected index case in the absence and presence of control measures. This model indicated no decline in Re in Liberia until the end of August 2014, and a drop in Re in Sierra Leone to around unity, which would signal the termination of the epidemic, by the end of July 2014. Based on viral genetic sequencing data collected in an early period of the outbreak in Sierra Leone (until 18 June 2014), Stadler et al.14 developed probabilistic SEIR models extending a birth-death model, as well as a deterministic coalescent model, and obtained median estimates of R0 in the range of 1.65-2.18.
Herein, we investigate the epidemic dynamics of EVD in Liberia and Sierra Leone from May 27 to December 21, 2014, using an agent-based model whose dynamics evolve on small-world networks of sizes equal to the population of each country. The model takes into account the main epidemiological factors, including the effect of burial practices, to virus transmission. The most recent data (see Methods) are fitted to the model, employing the so-called Equation-Free approach15 , to obtain estimations of the expected structure and density of the underlying transmission network, the mean time from the onset of symptoms to death or to recovery, the case fatality rate and the per-contact transmission probability. Using the agent-based simulator, we also estimate the expected effective reproductive number Re. By monitoring the evolution of the epidemic parameters and network structure, we projected the evolution of the epidemic until early March 2015 (10 weeks after December 21). We show that the epidemic is at the stage of saturation in Liberia and, based on our analysis of publicly available data, we expect it to fade out by early March. On the contrary, in Sierra Leone the epidemic seems to be ongoing. However, an up-to-date analysis of the epidemic dynamics for Sierra Leone, revealed a significant change towards slower transmission rates in the very last period (i.e. between December 21, 2014-January 18, 2015) as reflected by the mean Re of around 0.82.
METHODS
Development of an agent-based model
We have developed an agent-based model with individuals that interact through a small-world network constructed using the Watts & Strogatz (W&S) algorithm16 with a variable edge density. The edge density is defined as the number of links divided by the total possible links. In our model configuration, the density of connections can be adjusted at will. The construction of the network is based on random “rewiring” of links: starting with a ring network with
neighbors per node (
) with probability
, an existent edge between a node and its first nearest neighbor (in a clock- or counter clock-wise sense) is cut and rewired with a randomly selected node. Self-connection or duplicate connections are not allowed. This process is repeated for each node and its first nearest neighbors. For
the initial ring is invariant, while for
the network is completely random. For intermediate values,
, the network fluctuates between a regular and a random network, exhibiting the “small-world” property characterized by relatively small path lengths and high clustering coefficients. The network density denoted by “α” and defined as the ratio of the number of connections to the number of possible connections, is adjusted by randomly adding or subtracting the required number of links.
Agents can be in one of the following five discrete states:Susceptible , Exposed
, Infected
, Dead of the disease but not yet buried
, and
infectious state includes agents who die but whose burial entails risk for onward virus transmission. The contact network is denoted by
, where
is the set of vertices corresponding to the
agents, and
is the set of edges, i.e. the links between agents. An edge
is defined by
, where
are the agents associated with it;
if
are connected, and
otherwise. Here, all links are bidirectional and self-contacts are not allowed, i.e.
. The neighborhood of agent
is symbolized
. The system’s state over the set of the nodes (edges) is represented by
, where
is the set of the states of agent
.
The shown probabilities reflect the rates of progression from one stage to the next. Agents dead of the disease that have not been buried yet (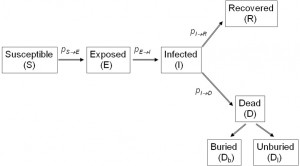
Fig. 1: Schematic of the Ebola virus infection states according to our proposed model.
) remain potentially infectious, while virus transmission stops with dead agents that have been buried safely (
). The inverse of the probability
that determines the rate by which an exposed agent becomes infectious, corresponds to the incubation period, i.e. the time from exposure to symptoms onset. This rate of incubation period is considered to be constant, set at
, as reported by the Who Ebola Response Team.27 The inverse of the probability
that determines the rate by which an infected agent dies of the disease, represents the time from symptoms onset to death.
This first rule simply sets the time period from death to burial to two days, during which family members and loved ones may be infected due to physical contact with the dead, still-contagious body.
The second rule implies that a susceptible agent gets exposed to the disease with a rate determined by the probability per infected contact (still alive or dead, but not yet buried). Our model cuts the long-range links of a dead, potentially infectious agent, reflecting the fact that only relatives and close community members can be infected during unsafe funeral practices and rites.
The third rule implies that an exposed agent becomes infectious with a rate determined by the probability, whose inverse corresponds to the incubation period, i.e. the time from exposure to symptoms onset.
Finally, an agent dies of the disease with a rate determined by the probability (whose inverse is the time from symptoms onset to death):
Alternatively, an agent could recover with a rate determined by the probability :
Rules (4) and (5) define the case fatality rate, say , which is the ratio of deaths to the infected population.The above framework bypasses the need of derivation of closures for the emergent population-level equations, thereby providing a systematic, computationally strict approach for macroscopic-level analysis.
Coarse-graining the agent-based dynamics for optimization and projection in time: the Equation-Free approach
Over the past years it has been shown that a new multi-scale computational framework, namely the Equation-Free approach, can be used to establish synergism between “conventional” numerical analysis, system identification and optimization techniques, on one hand, and microscopic complex systems modeling, on the other. This computational methodology allows the extraction of “large-scale, system-level” information from very large-scale microscopic/stochastic simulators more efficiently than with current methods. Briefly, the Equation-Free methodology consists of the following steps:15,17,18,19,20,21
(a) Choose the statistics of interest for describing the long-term behavior of the system and an appropriate representation for them. This could be, for example, the average numbers of susceptible, exposed, infected, and recovered individuals. This continuum description is called . These choices determine a restriction operator from the individual-based description
to the continuum description
.
(b) Choose an appropriate lifting operator from the continuum description to the individual-based description
. For example,
could make random node assignments, consistent with the continuum statistics. Note that
, that is, lifting from the continuum to the individual-based description, then restricting down again has no effect, apart from rounding-off effects.
(c) Prescribe a continuum initial condition .
(d) Transform this initial condition through lifting to one (or more) consistent individual-based realizations .
(e) Evolve this (these) realization(s) using the individual-based model for a desired time , generating
.
(f) Obtain the restrictions .
Steps (a) to (f), constitute the coarse time-stepper, or as otherwise called the coarse time-T map that, given an initial coarse-grained state of the system ,
at time
will report the result of the integration of the individual-based rules after a given time-horizon T (at time
),
, where
having
as initial condition;
denotes the vector of the system parameters.
The coarse time-stepper can be also used to perform coarse projective integration to forecast the coarse-grained dynamics after a certain time horizon. The basic idea is that the coarse time-stepper can be used to approximate the time derivatives of the corresponding continuum formulation, even if the continuum equations are not known in closed form. Specifically, the following steps are executed:15
(f) Repeat step (d) over several time steps, giving several as well as their restrictions
.
(g) Use the chord connecting these successive time-stepper output points to estimate the derivative of the continuum variables. Note that this step does not require knowledge of the explicit continuum equations.
(h) Use this derivative in an outer integrator (such as an autoregressive (ARX) model) to estimate the continuum state much later in time.
(i) Go back to step (b).
The above framework bypasses the need of derivation of closures for the emergent population-level equations, hence providing a systematic, computationally strict approach for macroscopic-level analysis. Through appropriate calls of the agent-based simulator, one can estimate the same information that a continuum closed model would allow to evaluate if this model was available as an explicit formula. Using this framework, steady state and stability computations as well as projective integration (forecasting) and optimization of the complex-emergent dynamics can be performed in a fully computational manner, bypassing the need of analytical derivation of closures for the macroscopic-level equations. Thus, the methodology provides a closure on demand for the unavailable macroscopic dynamics. The hypothesis that has to be fulfilled for the implementation of the methodology is that a coarse-grained model for the dynamics at the macroscopic/continuum level in principle exists and closes in terms of a few coarse-grained variables, which are usually the low-order moments of the microscopically evolving distributions and simultaneously the apparent observables of the evolving phenomenon.
In this work, we demonstrate how the Equation-Free framework can be used to effectively analyze certain aspects of the dynamics of the agent-based Ebola virus epidemic simulator. It is assumed that the emergent dynamics can be effectively described by the zero-order moments of the evolving distributions, i.e. the expected values of . We employ the framework (a) to optimize the model parameters to fit the reported outbreak data, and, (b) to forecast the dynamics of the epidemic in the future. More specifically, two network characteristics and four epidemic rates are the model parameters to be fitted. The network characteristics are the switching rewiring probability for constructing the small-world network,
, and the density of the network, say
, which is adjusted at will by adding or subtracting the required number of links at a portion determined by the gaining factor
;
is the density of the network constructed with the W&S algorithm
. Hence, the model parameters that are fitted are:
,
,
,
,
,
. The rate of incubation period is taken to be constant set as as
reported by the Who Ebola Response Team.21
The expected averaged values of the agents’ states are computed over
network realizations, and
simulations for each one of the network realizations. A coarse-grained observable/product of the above representation is also the coarse-grained effective reproductive ratio,
, defined as the average number of secondary infections produced by a typical infective person.
Population estimates, outbreak data and the simulation process
Based on the demographics reported by the United Nations (UN), the population estimates of Liberia and Sierra Leone are taken to be 4.2 and 6 million, respectively.22 Time series of the official case counts from the World Health Organization were used for model fitting.4 Case data, which included cumulative incidence and cumulative deaths by date of report for Liberia and Sierra Leone retrieved on 5th of January, were found on Wikipedia23 and compiled from WHO case reports. These data sets, which do not distinguish between suspect, probable and laboratory-confirmed case counts, are considered to represent the best available estimates of the current state of the epidemic in the two severely afflicted West African countries.
Simulations were performed using May 27, 2014 as an initial date and a time horizon of 70 days (10 weeks) with an equal sliding window time interval; the last date was December 21, 2014. Thus, fitted values of the network and model parameters as well as estimates of the effective reproductive ratio were computed in sequences of succeeded time intervals of 70 days. The trust-region-reflective approach for nonlinear minimization was implemented for parameter estimation.24 We used Matlab as our simulation environment.25
RESULTS
Figs. 2 & 4 show the cumulative numbers of infected and dead predicted by the model compared to the reported cases in Liberia and Sierra Leone, respectively. As shown, the proposed approach succeeds in approximating the reported data for both afflicted West African countries. Panels (a) of Figs. 3 & 5 depict the evolution of the estimated network characteristics, Expected cumulative cases of infected (dotted red) and dead (dotted black). WHO data are depicted by solid lines. The period under study has been tessellated into three windows with a length of 10 weeks each. For each window, the model parameters are estimated based on the data reported from WHO. and
, while panels (b-e) portray the model parameters
,
,
, and
that fit best to the reported Ebola virus epidemic dynamics in the two countries. The evolution of the estimated effective reproductive number, in Liberia and Sierra Leone is shown in panels (f) of Figs. 3 & 5, correspondingly.
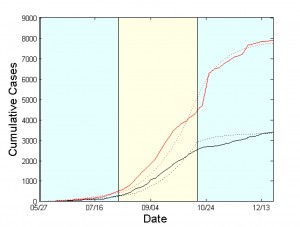
Fig. 2: Simulation Results for Liberia from May 27 to December 21, 2014.
The case of Liberia
The contact network exhibits a rather random structure with a rewiring switching probability (a) Evolution of contact network characteristics, switching probability of ~0.98 that remains constant during the whole period under study (Fig.3a). The density ratio of the network as represented by
, on the other hand, appears to be constant, at ~0.70, during the first two study periods; then, in the period from mid October to December 21, it drops to ~0.55 (Fig.3a), reflecting a sparser network structure that can possibly be attributed to population isolation policies.
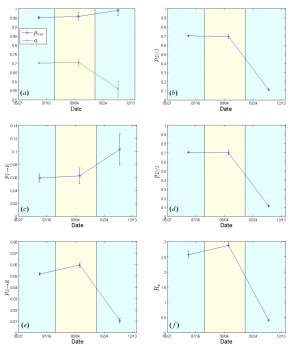
Fig. 3: Estimated model parameters for Liberia from May 27 to December 21, 2014.
, density ratio of the transmission network (a). (b) Case fatality rate
. (c) 1/{recovery period}
. (d) 1/{period from inset of symptoms to death}
. (e) Per-contact transmission probability
. (f) Effective Reproductive number
. 95% confidence intervals are also shown.
The case fatality rate that was estimated to be ~70% for the period extending from May 27 to mid October, dropped to ~10% subsequently (mid October-December 21) [Fig.3b]. The estimated recovery period (i.e. the inverse of
) was ~17 days (until mid October) and ~10 days in the last study period (until December 21) [Fig.3c]. The corresponding values for the expected period from the onset of symptoms to death (i.e. the inverse of
) were calculated to be ~8 days (May 27-mid October), and ~5 days in the last period (mid October-December 21) [Fig.3d]. The values of the per-contact transmission probability
, are shown in Fig.3e; they range from 0.05 (May 27-early August) to 0.01 most recently (mid October-December 21). The corresponding estimates of the effective reproductive number,
, were ~2.5 (May 27-early August), rising to ~2.8 (early August-mid October), dropping sharply to ~0.42 in the last period (mid October-December 21) [Fig.3f], thus indicating a saturation of the epidemic.
In summary, using the expected values of model parameters, as computed in the last period, we estimate that if the reported data correspond to the real situation, the current epidemic should fade out in Liberia until early March 2015.
Expected cumulative cases of infected (dotted red) and dead (dotted black). WHO data are depicted by solid lines. The period under study has been tessellated into three windows with a length of 10 weeks each. For each window, the model parameters are estimated based on the data reported from WHO.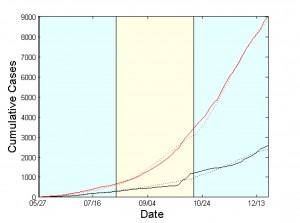
Fig. 4: Simulation Results for Sierra Leone from May 27 to December 21, 2014.
The case of Sierra Leone
Similarly to the case of Liberia, the contact network of Sierra Leone exhibits a rather random structure with a rewiring switching probability (a) Evolution of contact network characteristics, switching probability of ~0.98 that is kept constant during the study period (Fig.5a). The density ratio of the network as represented by
appears to be ~0.70 during the first period (May 27-early August), dropping to ~0.58 in the last two periods (early August-December 21) [Fig.5a].
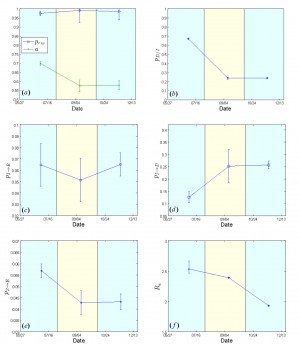
Fig. 5: Estimated model parameters for Sierra Leone from May 27 to December 21, 2014.
, density ratio of the transmission network (a). (b) Case fatality rate
. (c) 1/{recovery period}
. (d) 1/{period from inset of symptoms to death}
. (e) Per-contact transmission probability
. (f) Effective Reproductive number
. 95% confidence intervals are also shown.
The case fatality rate that was estimated to be ~67% for the period extending from May 27 to early August, dropped to ~24% from early September onwards (Fig.5b). The estimated recovery period (i.e. the inverse of
) fluctuated slightly from ~15 days (May 27-early August) up to ~20 days (early August-mid October) and then returned to the originally estimated value of ~15 days in the last period (mid October-December 21) [Fig.5c]. The expected period from the onset of symptoms to death (i.e. the inverse of
) was calculated to be ~8 days for the period between May 27 and early August, and ~4 days for the period between early August and December 21 (Fig.5d). Per-contact transmission probability values,
, dropped from 0.057 (May 27-early August) to ~0.043 from early August onwards (Fig.5e). The corresponding estimates of the effective reproductive rate,
, were ~2.5 (May 27-early August), ~2.4 (early August-mid October) and ~1.9 in the last period (mid October-December 21) [Fig.5f], thereby indicating a still ongoing outbreak.
In order to forecast the evolution of the Ebola virus epidemic in Sierra Leone, we followed the coarse projection procedure described in the Methods. For that purpose, we extrapolated the values of the model’s parameters as estimated within the last two periods; the resulting parameter values were then fed to the simulator using as coarse initial conditions the values of as computed on December 21. Based on the above procedure, we estimate that if the reported data correspond to the real situation, the expected cumulative number of infected cases may reach as high as 18,000 in early March, while the cumulative number of dead may reach as high as 5,000.
A summary of the estimated epidemiological parameters with their 95% confidence intervals for both countries is given in Table 1.
prw, Rewiring switching probability; CFR, Case fatality rate (pD/I); Re, Effective reproductive number
Liberia
Sierra Leone
Period
Variable
Mean
95% CI
Mean
95% CI
Early(May 27-August 4)
prw
0.95
0.94-0.96
0.97
0.96-0.98
Network density (α)
0.70
0.69-0.71
0.70
0.69-0.71
Time to death (Days)
8.7
8.5-9.0
7.9
6.7-9.6
Time to recovery (Days)
17
15.3-18.9
15.5
12.0-21.7
CFR (%)
70.2
70.0-70.4
66.8
65.7-67.8
Re
2.5
2.4-2.7
2.5
2.4-2.7
Middle(August 5-October 13)
prw
0.96
0.93-0.98
0.99
0.92-1.0
Network density (α)
0.70
0.69-0.72
0.57
0.54-0.61
Time to death (Days)
8.0
7.0-9.3
4.0
3.1-5.4
Time to recovery (Days)
16.0
13.5-19.8
19.6
14.2-30.9
CFR (%)
69.5
67.2-71.8
24.0
22.9-25.0
Re
2.9
2.8-3.0
2.4
2.3-2.5
Last(October 14- December 21)
prw
0.99
0.96-1.0
0.98
0.94-1.0
Network density (α)
0.56
0.52-0.60
0.58
0.55-0.60
Time to death (Days)
5.0
4.3-6.0
3.9
3.7-4.1
Time to recovery (Days)
9.7
7.9-12.7
15.4
13.3-18.2
CFR (%)
11.5
10.5-12.5
24.1
23.5-24.8
Re
0.42
0.41-0.43
1.93
1.92-1.94
Update to the case of Sierra Leone
Since the results we obtained by analyzing the reported data until December 21, 2014 showed that the epidemic was sustained in Sierra Leone, we decided to investigate further the current trends of the epidemic dynamics. Therefore, we expanded our analysis by taking into account the reported data for the country for the very last period (December 21, 2014-January 18, 2015). The results of this expanded analysis, which are indicative of a declining trend in the transmission potential of the virus, are shown in Table 2. Our analysis for this last period derived the following outcomes: rewiring switching probability ~ 0.70 (95% CI: 0.61-0.78), density ratio of the network
~0.58 (95% CI:0.48-0.68), expected period from the onset of symptoms to death ~3.7 days (95% CI: 2.9-5.2 days), expected period from the onset of symptoms to recovery ~8.9 days (95% CI: 5.5-23 days), per-contact transmission probability ~0.03 (95% CI: 0.02-0.04), case fatality rate ~33% (95% CI: 30-35%), effective reproductive number,
~ 0.82 (95% CI: 0.81-0.83).
prw, Rewiring switching probability;
, Per contact transmission probability; CFR, Case fatality rate (pD/I); Re, Effective reproductive number
Period
Variable
Mean
95% CI
Most recent
(December 21, 2014-January 18, 2015)prw
~0.70
0.61-0.78
Network density (α)
~0.58
0.48-0.68
Time to death (Days)
~3.7
2.9-5.2
Time to recovery (Days)
~8.9
5.5-23
pS→E
~0.03
0.02-0.04
CFR (%)
~33
30-35
Re
~ 0.82
0.81-0.83
DISCUSSION
To approximate the dynamics of the current EVD epidemic in Liberia and Sierra Leone from an early date (May 27) to December 21, 2014, we propose the use of an agent-based model. The dynamics of the model evolve on a small-world network,16 the size of which matches the demographics of each country, while its density is adjustable to account for the impact of interventions. By exploiting the Equation-Free framework for multi-scale analysis,15 we estimated the evolution of the structure and the density of the EBOV transmission network that best fitted the data reported by WHO for the cumulative number of infected cases and deaths. Estimates for the major epidemiological parameters of the model were also derived using a sliding window of 10 weeks with an equal sliding step. Using this information, we also performed a projection in time and provide an estimate for the potential cumulative number of cases until early March 2015. The originality of our study stems from the fact that our model and analysis take into account the heterogeneity in the interactions of the agents within the network. This unique property is reflected on the plasticity of the resulting transmission network as well as on the variability of the network density, which changes over time in response to public health intervention policies and the behavioral responses of individuals as the epidemic evolves. The methodological approach succeeded in approximating the reported data of cumulative numbers of infected and dead in both afflicted West African countries.
For Liberia and Sierra Leone, our estimates of the effective reproductive number , which provides a measure of the potential of EVD transmission, as well as the estimates of the other key epidemiological variables, are quite close to the ones reported by the WHO Ebola Response Team and other groups. Transmissibility estimates from previous studies indicated an overall reproductive number
ranging from 1.5 to 2.0 in West Africa in the early period of the epidemic.12,26 For Sierra Leone, in particular, the
estimate of ~2.5 that we obtained in the early period of the epidemic (May 27-early August) agrees well with the estimated
of ~2 to 2.5 given by the WHO Ebola Response Team and others.13,14,27 Rivers et al.10 had calculated a lower
of 1.78 for the same period in Sierra Leone. Our analysis revealed that
remains well above 1 for the duration of the study period in Sierra Leone (~2.4 for the middle period from early August-mid October and ~1.9 for the last period extending from mid October to December 21). These values that are well above unity are indicative of an ongoing epidemic with a sustained transmission potential in Sierra Leone.
The situation appears to be different in the neighboring Liberia, where intervention policies seem to become effective after mid October, when a sharp decrease in new infections and deaths is observed. Accordingly, we estimated an of ~2.5 in the early period (May 27-early August), rising to ~2.9 in the middle period (early August-mid October) before dropping sharply to ~0.4 in the last study period (mid October-December 21). Chowell et al.7 also reported a declining trend from 2.4 in early August, to 1.6 around September 6, to 1.3 by October 1 for the Liberian . Consistent with our early period estimate of ~2.5,
values in the range of 2.2 to 2.5 were computed for that time interval by two other groups;10,28 others estimated
to be lower, ranging from 1.6 to 1.8, during the early phase of the epidemic.13,27 For Liberia we estimate that the epidemic did not reach a saturation point before early October.
Additional notable differences in the estimated epidemiological profiles of the two countries from the early (May 27-early August) to the last study period (mid October- December 21) include: (i) nearly steady mean times to recovery from symptoms onset of ~15.4 days, with an intermediate increase to 19.6 days in the middle period (early August-mid October), in Sierra Leone vs. reduced from 17 to 9.7 days, with an intermediate value of 16 days, in Liberia; and (ii) lower reductions in the case fatality rate (from 66.8% to 24.1% in Sierra Leone vs. from 70.2% to 11.5% in Liberia) with dissimilar corresponding intermediate estimates of 24%vs. ~69.5%. Our estimates for the case fatality rate in the two countries are close to the numbers reported by the WHO Ebola response team for approximately the same period of reference (May 27-mid October); more specifically, we estimated the case fatality rate to be ~70.2% (95% CI, 70.0-70.4%) in Liberia and ~66.8% (95% CI, 65.7-67.8%) in Sierra Leone for this time period, while the WHO team had reported corresponding values of 72.3% (95% CI, 68.9-75.4) in Liberia and ~69.0% (95% CI, 64.5-73.1%) in Sierra Leone.27
Less pronounced differences between the two West African countries were found in the trends over time for the mean time from symptoms onset to death. In particular, for Liberia we estimated the mean time from symptoms onset to death to be about 9 days for the early period of May 27-mid October (the WHO team had reported a mean value of 7.9, yet with a large standard deviation), and 5 days for the last period from mid-October to December 21. For Sierra Leone, we estimated the mean time from symptom onset to death to be around 8 days for the early epidemic period from May 27 to early August (the WHO team had reported a mean value of 8.6, again with a large standard deviation), and around 4 days for the last period from mid-October to December 21.
At this point we should note that the findings of this work are subject to several limitations. The first and most important one is related to the quality and accuracy of the outbreak data that were fed to the proposed mathematical model compared to the real figures. Underreporting is certainly to be expected.29 Furthermore, as explained in the Methods, these data-sets do not distinguish between suspect, probable and laboratory-confirmed case counts. They are nonetheless considered to represent the best available estimates of the current state of the epidemic in the two severely afflicted West African countries.
We also performed a projection in time (10 weeks after December 21, 2014) of the EVD epidemic dynamics. Based on our approach, we estimate that the epidemic is already saturated in Liberia and it seems that it will be under control by March 2015. As reported recently,30 the movement and mixing of infected and uninfected patients in hospitals at the early stage of the outbreak was the driving force of the epidemic in Liberia.The subsequent decrease of incidence in the country is presumably attributable to the increasing availability of Ebola treatment units (which in turn contributed to drastically decreased hospital transmission), safe burials, and distribution of household protection kits.30 In contrast, the epidemic is sustained in Sierra Leone, with no evidence of slowing down at least until December 21, particularly as shown by the current effective reproductive number that remains well above unity. Based on the analysis before December 21, we predict that the cumulative number of cases in the country could reach as high as 18,000 and the cumulative number of deaths might exceed 5,000, by early March, if drastic control measures to curtail the epidemic are not taken. However, based on the analysis using the most recenlty reported data (December 21, 2014-January 18, 2015) our estimate for the effective reproductive number falls below unity (~0.82) indicating a different tendency compared to the previous period towards a decreased transmission potential in Sierra Leone. This decrease in is accompanied by a drop of an order of 28% in the switching rewiring probability of the transmission network rendering its structure more clustered, with less long-range connections between individuals.
The biological characteristics of the virus as well as the epidemiological features associated with its transmission are similar to those observed in previous outbreaks and, therefore, cannot account for the unprecedented scale of the current EVD epidemic in West Africa.27 The rapid institution of control measures (as detailed for example, in, Legrand et al.9 and WHO,27)is key to halt the spread of such a deadly infection.
References
- Baize S, Pannetier D, Oestereich L, Rieger T, Koivogui L, Magassouba N, Soropogui B, Sow MS, Keïta S, De Clerck H, Tiffany A, Dominguez G, Loua M, Traoré A, Kolié M, Malano ER, Heleze E, Bocquin A, Mély S, Raoul H, Caro V, Cadar D, Gabriel M, Pahlmann M, Tappe D, Schmidt-Chanasit J, Impouma B, Diallo AK, Formenty P, Van Herp M, Günther S. Emergence of Zaire Ebola virus disease in Guinea. N Engl J Med. 2014 Oct 9;371(15):1418-25. PubMed PMID:24738640.
- Gire SK, Goba A, Andersen KG, Sealfon RS, Park DJ, Kanneh L, Jalloh S, Momoh M, Fullah M, Dudas G, Wohl S, Moses LM, Yozwiak NL, Winnicki S, Matranga CB, Malboeuf CM, Qu J, Gladden AD, Schaffner SF, Yang X, Jiang PP, Nekoui M, Colubri A, Coomber MR, Fonnie M, Moigboi A, Gbakie M, Kamara FK, Tucker V, Konuwa E, Saffa S, Sellu J, Jalloh AA, Kovoma A, Koninga J, Mustapha I, Kargbo K, Foday M, Yillah M, Kanneh F, Robert W, Massally JL, Chapman SB, Bochicchio J, Murphy C, Nusbaum C, Young S, Birren BW, Grant DS, Scheiffelin JS, Lander ES, Happi C, Gevao SM, Gnirke A, Rambaut A, Garry RF, Khan SH, Sabeti PC. Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak. Science. 2014 Sep 12;345(6202):1369-72. PubMed PMID:25214632.
- Ebola haemorrhagic fever in Zaire, 1976. Bull World Health Organ. 1978;56(2):271-93. PubMed PMID:307456.
- http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/
Reference Link - Siettos CI, Russo L. Mathematical modeling of infectious disease dynamics. Virulence. 2013 May 15;4(4):295-306. PubMed PMID:23552814.
- Reppas AI, Spiliotis KG, Siettos CI. Epidemionics: from the host-host interactions to the systematic analysis of the emergent macroscopic dynamics of epidemic networks. Virulence. 2010 Jul-Aug;1(4):338-49. PubMed PMID:21178467.
- Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J Theor Biol. 2004 Jul 7;229(1):119-26. PubMed PMID:15178190.
- Lekone PE, Finkenstädt BF. Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics. 2006 Dec;62(4):1170-7. PubMed PMID:17156292.
- Legrand J, Grais RF, Boelle PY, Valleron AJ, Flahault A. Understanding the dynamics of Ebola epidemics. Epidemiol Infect. 2007 May;135(4):610-21. PubMed PMID:16999875.
- Rivers CM, Lofgren ET, Marathe M, et al. Modeling the impact of interventions on an epidemic of Ebola in Sierra Leone and Liberia. PLOS Currents Outbreaks. 2014 Oct 16. Edition 1. doi: 10.1371/currents.outbreaks.fd38dd85078565450b0be3fcd78f5ccf.
- Kiskowski MA. A three-scale network model for the early growth dynamics of 2014 West Africa Ebola epidemic. PLOS Currents Outbreaks. 2014 Nov 13. Edition 1. doi: 10.1371/currents.outbreaks.c6efe8274dc55274f05cbcb62bbe6070.
- Gomes MFC, Pastore y Piontti A, Rossi L, et al. Assessing the international spreading risk associated with the 2014 West African Ebola outbreak. PLOS Currents Outbreaks. 2014 Sep 2. Edition 1. doi: 10.1371/currents.outbreaks.cd818f63d40e24aef769dda7df9e0da5.
- Althaus CL. Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. PLOS Currents Outbreaks. 2014 Sep 2. Edition 1. doi: 10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288.
- Stadler T, Kühnert D, Rasmussen DA, et al. Insights into the early epidemic spread of Ebola in Sierra Leone provided by viral sequence data. PLOS Currents Outbreaks. 2014 Oct 6. Edition 1. doi: 10.1371/currents.outbreaks.02bc6d927ecee7bbd33532ec8ba6a25f.
- Kevrekidis IG, Gear CW, Hyman JM, et al. Equation-free coarse-grained multiscale computation: enabling microscopic simulators to perform system-level tasks. Communications in Mathematical Sciences 2003; 1(4): 715–762.
- Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks. Nature. 1998 Jun 4;393(6684):440-2. PubMed PMID:9623998.
- Makeev A, Maroudas D, Kevrekidis I G. Coarse stability and bifurcation analysis using stochastic simulators: Kinetic Monte Carlo Examples. J. Chemical Physics. 2002; 116: 10083-10091.
- Gear CW, Kevrekidis IG, Theodoropoulos K. Coarse integration/bifurcation analysis via microscopic simulators. Comput. Chem. Engng. 2002; 26: 941-963.
- Theodoropoulos K., Qian Y-H, Kevrekidis IG. Coarse stability and bifurcation analysis using timesteppers: a reaction-diffusion example. PNAS. 2002; 97: 9840-9843.
- Siettos CI, Graham MD, Kevrekidis, IG. Coarse Brownian dynamics for nematic liquid crystals: bifurcation diagrams via stochastic simulation. J. Chem. Phys. 2003; 118: 10149.
- Kevrekidis IG, Gear CW, Hummer G. Equation-free: the computer-assisted analysis of complex, multiscale systems. AI.Ch.E. J. 2004; 50: 1346-1354.
- http://data.un.org/
Reference Link - Wikipedia, “Timeline of reported cases and deaths, Ebola virus epidemic in West Africa,” 2014
- Coleman TF, Li Y. An interior, trust region approach for nonlinear minimization subject to bounds. SIAM Journal on Optimization. 1996; 6: 418–445.
- http://www.mathworks.com
Reference Link - Fisman D, Khoo E, Tuite A. Early epidemic dynamics of the West African 2014 Ebola outbreak: estimates derived with a simple two-parameter model. PLOS Currents Outbreaks. 2014 Sep 8. Edition 1. doi: 10.1371/currents.outbreaks.89c0d3783f36958d96ebbae97348d571.
- Who Ebola Reponse Team. Ebola virus disease in West Africa--the first 9 months of the epidemic and forward projections. N Engl J Med. 2014; 371(16): 1481-1495. doi: 10.1056/NEJMoa1411100. Epub 2014 Sep 22.
- Lewnard JA, Ndeffo Mbah ML, Alfaro-Murillo JA, et al. Dynamics and control of Ebola virus transmission in Montserrado, Liberia: a mathematical modelling analysis. Lancet Infect Dis. 2014; 14(12): 1189-1195. doi: 10.1016/S1473-3099(14)70995-8. Epub 2014 Oct 23.
- Meltzer MI, Atkins CY, Santibanez S, et al. Estimating the future number of cases in the Ebola epidemic: Liberia and Sierra Leone, 2014–2015. MMWR Surveill Summ 2014; 63: 2014–15
- Merler S, Ajelli M, Fumanelli L, Gomes MF, Piontti AP, Rossi L, Chao DL, Longini IM Jr, Halloran ME, Vespignani A. Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: a computational modelling analysis. Lancet Infect Dis. 2015 Jan 6. PubMed PMID:25575618.
Leave a Comment
You must be logged in to post a comment.